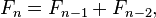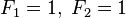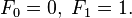斐波那契数列(fabnacci)java实现
斐波那契数列定义:From Wikipedia, the free encyclopedia
http://en.wikipedia.org/wiki/Fibonacci_number
In mathematics, the Fibonacci numbers or Fibonacci sequence are the numbers in the following integer sequence:[2][3]
or (often, in modern usage):
By definition, the first two numbers in the Fibonacci sequence are 1 and 1, or 0 and 1, depending on the chosen starting point of the sequence, and each subsequent number is the sum of the previous two.
In mathematical terms, the sequence Fn of Fibonacci numbers is defined by the recurrence relation
or[4]
本例以后一种为例:
最简单的一种:两层递归
public static long fibonacci(int n){
if(n==0) return 0;
else if(n==1) return 1;
else
return fibonacci(n-1)+fibonacci(n-2);
}
问题是:随着n的数值逐渐增多,时间和空间耗费太大,读者可以自行实验。在我的机器上n=50时就不能忍受了。
考虑优化:一层递归
public static void main(String[] args) {
long tmp=0;
// TODO Auto-generated method stub
int n=10;
Long start=System.currentTimeMillis();
for(int i=0;i<n;i++){
System.out.print(fibonacci(i)+" ");
}
System.out.println("-------------------------");
System.out.println("耗时:"+(System.currentTimeMillis()-start));
}
public static long fibonacci(int n) {
long result = 0;
if (n == 0) {
result = 0;
} else if (n == 1) {
result = 1;
tmp=result;
} else {
result = tmp+fibonacci(n - 2);
tmp=result;
}
return result;
}
递归时间减少了到不到50%
最好的方式,不使用递归的方式来做。
public static long fibonacci(int n){
long before=0,behind=0;
long result=0;
for(int i=0;i<n;i++){
if(i==0){
result=0;
before=0;
behind=0;
}
else if(i==1){
result=1;
before=0;
behind=result;
}else{
result=before+behind;
before=behind;
behind=result;
}
}
return result;
}
斐波那契数列(fabnacci)java实现的更多相关文章
- 几种复杂度的斐波那契数列的Java实现
一:斐波那契数列问题的起源 13世纪初期,意大利数论家Leonardo Fibonacci在他的著作Liber Abaci中提出了兔子的繁殖问题: 如果一开始有一对刚出生的兔子,兔子的长大需要一个月, ...
- 斐波那契数列【java实现】
java 实现斐波那契数列 以下是Java代码实现(递归与递推两种方式): import java.util.Scanner; /** * Fibonacci * * @author tongqian ...
- 斐波那契数列(Java)
一.什么是斐波那契数列 斐波那契数列(Fibonacci sequence),又称黄金分割数列.因数学家列昂纳多·斐波那契(Leonardoda Fibonacci)以兔子繁殖为例子而引入,故又称为& ...
- 剑指Offer-7.斐波那契数列(C++/Java)
题目: 大家都知道斐波那契数列,现在要求输入一个整数n,请你输出斐波那契数列的第n项(从0开始,第0项为0). n<=39 分析: 斐波那契数列是0,1,1,2,3,5,8,13...也就是当前 ...
- 从斐波那契数列看java方法的调用过程
先看斐波那契数列的定义: 斐波那契数列(Fibonacci sequence),又称黄金分割数列.因数学家列昂纳多·斐波那契(Leonardoda Fibonacci)以兔子繁殖为例子而引入,故又称为 ...
- (转)从斐波那契数列看Java方法的调用过程
斐波那契数列的定义: 斐波那契数列(Fibonacci sequence),又称黄金分割数列,因数学家列安纳多·斐波那契(Leonardoda Fibonacci)以兔子繁殖为例子而引入,故又称为“兔 ...
- 算法小节(一)——斐波那契数列(java实现)
看到公司的笔试题中有一道题让写斐波那契数列,自己忙里偷闲写了一下 什么是斐波那契数列:斐波那契数列指的是这样一个数列 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...
- 【斐波那契数列】java探究
题目描述 大家都知道斐波那契数列,现在要求输入一个整数n,请你输出斐波那契数列的第n项(从0开始,第0项为0). n<=39 解析 (1)递归方式 对于公式f(n) = f(n-1) + f(n ...
- 剑指offer第二版面试题10:斐波那契数列(JAVA版)
题目:写一个函数,输入n,求斐波那契数列的第n项.斐波那契数列的定义如下: 1.效率很低效的解法,挑剔的面试官不会喜欢 使用递归实现: public class Fibonacci { public ...
- HDU 5686 斐波那契数列、Java求大数
原题:http://acm.hdu.edu.cn/showproblem.php?pid=5686 当我们要求f[n]时,可以考虑为前n-1个1的情况有加了一个1. 此时有两种情况:当不适用第n个1进 ...
随机推荐
- 使用<span>标签为文字设置单独样式
这一小节讲解<span>标签,我们对<em>.<strong>.<span>这三个标签进行一下总结: 1. <em>和<strong& ...
- JS中区分参数方法
实现功能:在使用cocosjs制作游戏过程中,很多东西都可以重复使用,例如菜单栏等等.今天尝试写了一个自定义的Js文件用作菜单方便以后使用. 将菜单按钮,以及触发事件作为参数生成一个层 直接在游戏中使 ...
- JavaScript_object基础
之前写Java时老是有点蒙,大部分都是用jQuery,但原理还不是很清楚,最近一段时间在系统的学习JavaScript,有什么问题或错误请指出,多谢..................... Obje ...
- JS字符串常用方法
// 来自 http://www.runoob.com/js/js-strings.html var str01 = "odd open xboxone" , str02 ...
- C语言之头文件,static与const关键字
[前言] 最近几个月在做一个C语言代码重构的项目,过程中也让我对之前在书本上学习到的东西有些补充和巩固,在本博中总结记录下,梳理下零碎的知识点和经验也加深印象,书写是为了更好地思考.平时也都是用印象笔 ...
- javascript禁止输入数字
function onkeypressIsNumber(){ var mainForm = document.mainForm;//mainForm是form表单的ID for(var i=0; i& ...
- 一元云购完整源码 云购CMS系统 带安卓和ios手机客户端
看起来不错的一套一元云购CMS源码,源码包里面带了安卓和ios手机客户端,手机客户端需要自己反编译. 这里不做功能和其它更多的介绍,可以自己下载后慢慢测试了解. 下面演示图为亲测截图< ...
- Egret 事件机制
主要流程: private createGameScene():void { var JimGreen = new Boy(); var HanMeimei = new Girl(); JimGree ...
- Android添加桌面快捷方式的简单实现
核心代码如下: Button bn = (Button) findViewById(R.id.bn); // 为按钮的单击事件添加监听器 bn.setOnClickListener(new OnCli ...
- C51 延时程序
一.相关换算 1.1s=10^3ms(毫秒)=10^6μs(微秒)=10^9ns(纳秒)=10^12ps(皮秒)=10^15fs(飞秒)=10^18as(阿秒)=10^21zm(仄秒)=10^24ym ...


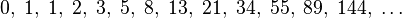 (sequence
(sequence