三层for循环求解组成三角形边的组合

假设a、b、c是三角形的三条边，当三条边符合勾股定理时，即，a²+b²=c² ，为直角三角形。若a、b、c均为小于等于50的整数，求能够组成直角三角形的所有组合。请显示边的各种可能组合情况，显示总的组合数量。注意：
    (a=3, b=4, c=5)
    (a=4, b=3, c=5)
    (a=5, b=4, c=3)
等情况只能算1种组合。

首先使用3个for循环

		int a,b,c;
		for(a=1;a<=50;a++){
			for(b=1;b<=50;b++ ){
				for(c=1;c<=50;c++){

				}
			}
		}

然后增加if判断，只要符合a*a+b*b=c*c，则输出组合，另外需要定义一个number的整除存储组合的个数。

public static void main(String args[]){

		int a,b,c,number=0;
		for(a=1;a<=50;a++){
			for(b=1;b<=50;b++ ){
				for(c=1;c<=50;c++){
					if((a*a+b*b)==c*c){
						System.out.println("(a="+a+",b="+b+",c="+c+")");
						number++;
					}
				}
			}
		}
		System.out.println("一共的组合数量"+number);
}

　　运行输出：

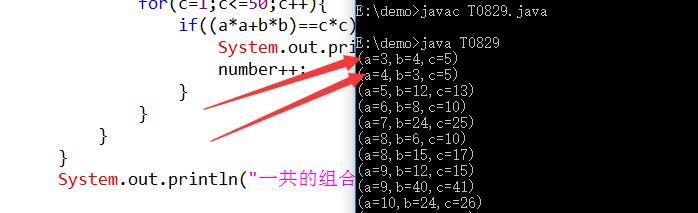
此时有重复的情况，重复的数据我们需要消除；

我们使用条件a>b

public static void main(String args[]){

		int a,b,c,number=0;
		for(a=1;a<=50;a++){
			for(b=1;b<=50;b++ ){
				for(c=1;c<=50;c++){
					if((a*a+b*b)==c*c && a>b){
						System.out.println("(a="+a+",b="+b+",c="+c+")");
						number++;
					}
				}
			}
		}
		System.out.println("一共的组合数量"+number);
}

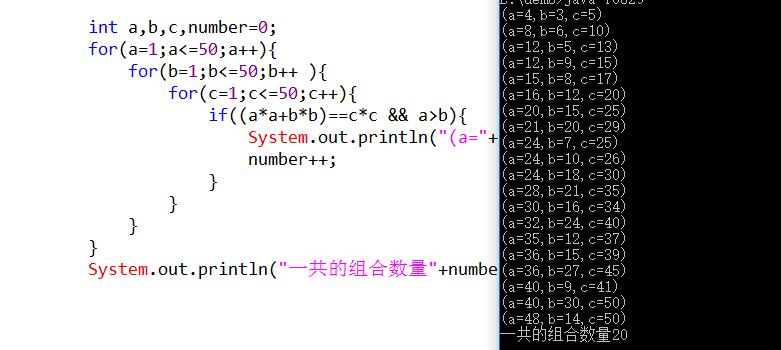
　　关键代码：if((a*a+b*b)==c*c && a>b){}

运行输出：