Monte Carlo Control
Problem of State-Value Function
Similar as Policy Iteration in Model-Based Learning, Generalized Policy Iteration will be used in Monte Carlo Control. In Policy Iteration, we keep doing Policy Evaluation and Policy Improvement untill our policy converging to Optimal Policy.

Every time when we improve the policy, the action that gives the best return(reward+value function of the next state) will be picked.
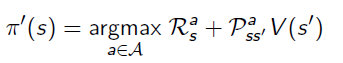
The problem of this algorithm if we directly transfering to Monte Carlo is: it is based on the Transition Matrix.
Monte Carlo Control based on Q function
The idea of Policy Iteration can be used to Estimite Action-Value Function, and it is very useful for Model-Free problem. The process of choosing actions does not depend on State-Value function, because the return from a specific action is given by Monte Carlo estimation.
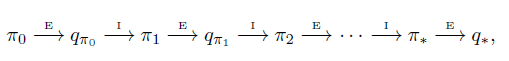

Q function can be updated by:
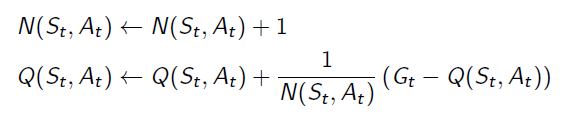
When we improve the policy, we just pick the action that produce the maximum Q value.
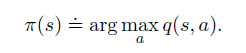
Exploration-exploitation Dilemma and ε-Greedy Exploration:
In Model-Based Policy Iteration algorithm, we update all State-Value function within a single policy evaluation process, so that we can choose the best actions from the whole action space whiled improving policies. Nevertheless, Monte Carlo Learning only updates the Action-Value functions whose actions were taken on the previous episode. So there are probabily some actions having better returns than the actions we have tried. Sometimes we need to give them a trial. We call that problem the Exploration-Exploitation Delemma.
It is necessary to try some new opened restaurant, rather than going to the usual place every day.
ε-Greedy Exploration is the algorithm that gives the agent probability=ε to choose randomly actions and 1-ε to stay on the optimal action.
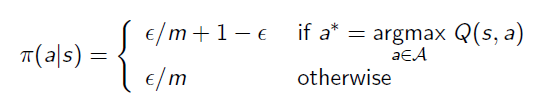
Monte Carlo Control的更多相关文章
- 增强学习(四) ----- 蒙特卡罗方法(Monte Carlo Methods)
1. 蒙特卡罗方法的基本思想 蒙特卡罗方法又叫统计模拟方法,它使用随机数(或伪随机数)来解决计算的问题,是一类重要的数值计算方法.该方法的名字来源于世界著名的赌城蒙特卡罗,而蒙特卡罗方法正是以概率为基 ...
- Monte Carlo Policy Evaluation
Model-Based and Model-Free In the previous several posts, we mainly talked about Model-Based Reinfor ...
- Monte Carlo方法简介(转载)
Monte Carlo方法简介(转载) 今天向大家介绍一下我现在主要做的这个东东. Monte Carlo方法又称为随机抽样技巧或统计实验方法,属于计算数学的一个分支,它是在上世纪四十年代 ...
- PRML读书会第十一章 Sampling Methods(MCMC, Markov Chain Monte Carlo,细致平稳条件,Metropolis-Hastings,Gibbs Sampling,Slice Sampling,Hamiltonian MCMC)
主讲人 网络上的尼采 (新浪微博: @Nietzsche_复杂网络机器学习) 网络上的尼采(813394698) 9:05:00 今天的主要内容:Markov Chain Monte Carlo,M ...
- Monte Carlo Approximations
准备总结几篇关于 Markov Chain Monte Carlo 的笔记. 本系列笔记主要译自A Gentle Introduction to Markov Chain Monte Carlo (M ...
- (转)Markov Chain Monte Carlo
Nice R Code Punning code better since 2013 RSS Blog Archives Guides Modules About Markov Chain Monte ...
- [其他] 蒙特卡洛(Monte Carlo)模拟手把手教基于EXCEL与Crystal Ball的蒙特卡洛成本模拟过程实例:
http://www.cqt8.com/soft/html/723.html下载,官网下载 (转帖)1.定义: 蒙特卡洛(Monte Carlo)模拟是一种通过设定随机过程,反复生成时间序列,计算参数 ...
- Introduction to Monte Carlo Tree Search (蒙特卡罗搜索树简介)
Introduction to Monte Carlo Tree Search (蒙特卡罗搜索树简介) 部分翻译自“Monte Carlo Tree Search and Its Applicati ...
- (转)Monte Carlo method 蒙特卡洛方法
转载自:维基百科 蒙特卡洛方法 https://zh.wikipedia.org/wiki/%E8%92%99%E5%9C%B0%E5%8D%A1%E7%BE%85%E6%96%B9%E6%B3%9 ...
随机推荐
- 流畅的Python (Fluent Python) —— 前言
本书重点: 这本书并不是一本完备的 Python 使用手册,而是会强调 Python 作为编程语言独有的特性,这些特性或者是只有 Python 才具备的,或者是在其他大众语言里很少见的. Python ...
- Apache 用户认证
基本认证(Basic) 摘要认证(Digest) 更安全 创建一个名为 users 的认证口令: htpasswd -c /usr/local/apache2/conf/users sam ...
- 继续死磕python
一.数据运算 算术运算 比较运算 赋值运算 逻辑运算 成员运算 身份运算 位运算 其中左右移运算是逻辑左右移即缺失位补0,而算数右移缺失补符号位(注意逻辑运算都是补码运算即都取补码再运算,然后结果也是 ...
- C#索引器2 字符串作为索引号
6.索引器 字符串作为索引号 public class Demo { private Hashtable name = new Hashtable(); public string this[st ...
- VS插件CodeRush for Visual Studio发布v18.2.9|附下载
CodeRush能帮助你以极高的效率创建和维护源代码.Consume-first 申明,强大的模板,智能的选择工具,智能代码分析和创新的导航以及一个无与伦比的重构集,在它们的帮助下能够大大的提高你效率 ...
- python的setup.py文件
最近工作需要,用Cython写了*.pyx扩展,并将其编译成C文件,最后转换为so扩展,供python引用使用 distutils 编译,建立一个setup.py 的脚本from distutils. ...
- flex的12个属性
容器(父元素)的属性: flex-direction属性决定主轴的方向 flex-wrap 属性决定项目在一行排不下的情况下是否换行 flex-flow flex-flow属性是flex-direct ...
- linux运维、架构之路-Docker快速入门
一.Docker介绍 Docker是Docker.lnc公司开源的一个基于LXC技术之上构建的Container容器引擎,源代码托管在Github上,基于Go语言并遵从Apache2.0 ...
- Shell入门02
Shell入门-02 1.重定向 标准输入(<) 标准输出 标准错误重回定向 程序 = 指令 + 数据 命令 变量 在程序中,数据如何输入?又如何输出? 数据输入:键盘 – 标准输入,但是并 ...
- prefetches
用于设置预请求的所有url的列表,该部分URL,会在进入小程序后自动发起请求(优于开发者代码加载).当开发者再次发起request请求时可以增加cache参数,如果配置的prefetch请求已返回,则 ...
