2019.7.9 校内交流测试（T 3 待更完）

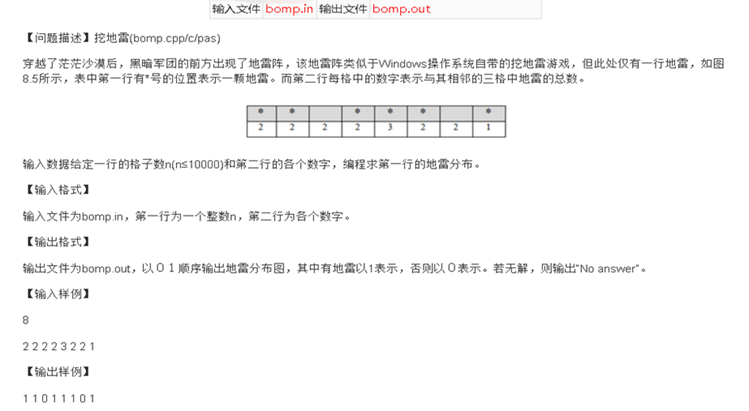
T1_挖地雷（提交文件bomp.cpp）

递推大法好啊

题解

递推高级题目

这个题就是按照扫雷的思路解决

相邻的三个格子上的雷数和加起来正好等于中间格子上的数

所以当我们确定了第一个格子周围的雷，其余的就都好解决了

注意不好确定的是当第一个格子的数字为1时候，可以在第一个格子上放雷，也可以在第二个格子上放雷，这两种情况可能一种有解，另一种无解

PS：今天这题毒瘤的很，首先谴责T1数据点18:2 1 1，答案不唯一啊！！！

代码

#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<cstdlib>
#include<queue>

using namespace std;

inline int read()
{
    int ans=;
    char last=' ',ch=getchar();
    while(ch<''||ch>'') last=ch,ch=getchar();
    while(ch>=''&&ch<='') ans=ans*+ch-'',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}

int n;
bool flag;
int pan[];
int ans[];

bool dtdfh()
{
    for(int i=;i<=n;i++)
    {
        ans[i+]=pan[i]-ans[i]-ans[i-];
        if(ans[i+]<||ans[i+]>) return ; //超额
    }

    if(ans[n+]>) return ;  //不该有数字的位置有了数字
    else return ;

}

int main()
{
    freopen("bomp.in","r",stdin);
    freopen("bomp.out","w",stdout);

    n=read();
    for(int i=;i<=n;i++)
    {
        pan[i]=read();
        if(pan[i]<||pan[i]>||(i==&&pan[i]>)||(i==n&&pan[i]>))  //输入不合法
        {
            printf("No answer\n");
            return ;
        }
    }

    //先确定第一个啊
    if(pan[]==) { ans[]=ans[]=; }
    if(pan[]==) { ans[]=;ans[]=; }
    if(pan[]==) { ans[]=ans[]=; }

    flag=dtdfh();  //递推求解
    if(pan[]==&&flag==)
    {
        ans[]=;ans[]=;
        flag=dtdfh();
    }

    if(!flag)   //无解
    {
        printf("No answer\n");
        return ;
    }

    else
    {
        for(int i=;i<=n;i++)
           printf("%d ",ans[i]);
    }

    return ;
}

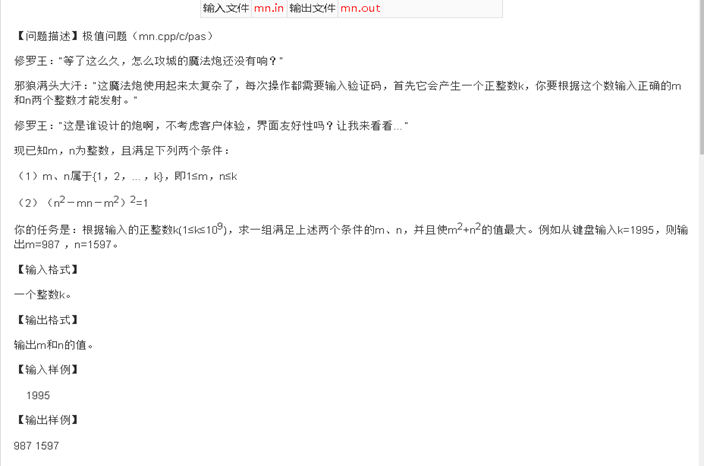
T2_极值问题（提交文件mn.cpp）

打表大法好啊

题解

我说这题是打表找规律发现是斐波那契数列QWQ

打表之后发现 m , n 是不超过k的两个相邻的最大斐波那契数

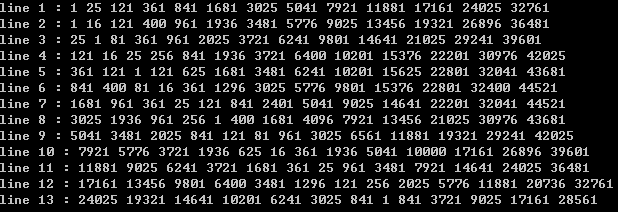
正解证明斐波那契，感谢这个大佬 “ 寄蜉蝣于天地，渺沧海之一粟 ”

证明一下啦：

首先我们看到题目给出的那个式子：

start：（n²-mn-m²）²=1

----> ： （m²+mn-n²）²=1

拿出括号里的单独看：    m²+mn-n² 

m²+mn-n² +2n²-2n²+mn-mn

（m+n）²-2n²-mn

（m+n）² -n²-n²-mn

（m+n）² -（m+n）n - n²

也就是：（n²-mn-m²）²  ---->   （m+n）² -（m+n）n - n²

so，如果我们有一组解 （m,n），那么一定还存在一组解 （n,m+n），所以你发现这就构成了斐波那契数列！！！

递推求解就好了！！！

代码

#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<cstdlib>
#include<queue>

using namespace std;

inline int read()
{
    int ans=;
    char last=' ',ch=getchar();
    while(ch<''||ch>'') last=ch,ch=getchar();
    while(ch>=''&&ch<='') ans=ans*+ch-'',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}

const int maxn=1e6+;
int k,m,n;
long long feibo[maxn]={,};

int main()
{
    freopen("mn.in","r",stdin);
    freopen("mn.out","w",stdout);
    k=read();

    for(int i=;i<=;i++)
    {
        feibo[i]=feibo[i-]+feibo[i-];
    }

    for(int i=;i<=;i++)
    {
        if(feibo[i]>k) {
            m=i-;
            n=i-;
            printf("%ld %ld\n",feibo[n],feibo[m]);
            return ;
        }
    }

    return ;
}

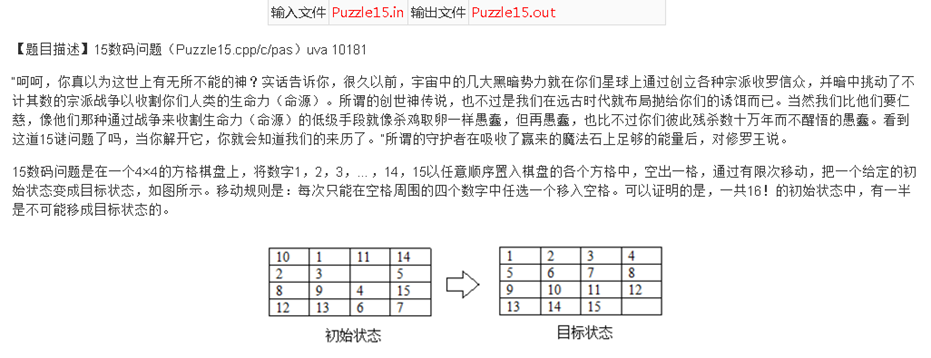
T3_15数码问题（提交文件Puzzle15.cpp）

骗分大法好啊

题解

说人话：编程50步求解15数码

这题数据水，偏分最高60

what is UVA？？？一个nice的oj

这个题目用到了神奇的 IDA* 算法（崩溃）

感谢百度找到一个大佬--恋恋恋恋吥舍--

链接： 原文：https://blog.csdn.net/baidu_30476939/article/details/53119195

首先了解一下几个概念：

1.逆序对：在一个序列里，如果一个数后面的数比他小，那么他们两个构成一个逆序对

有何用处？？判断一下有无解：

把初始矩阵从左到右，从上到下，展成一行，求它的逆序对 （显然目标矩阵的逆序对个数为0）

           于是这里用到一个定理：设初始状态0所在的行数为i,目标状态0所在的行数为j，两者之差的绝对值为k。若k为奇数，则初始矩阵与目标矩阵两个矩阵相应的逆序数的奇偶性相异才有解。若k为偶数，则两个矩阵的逆序数必须相同才有解。不是上述两种情况即为无解。通过初始判定就可以不用搜索就能直接否定无解情况。

转化到这个题上就是，K为奇数，矩阵逆序对数也应为奇数，K为偶数，矩阵逆序对数也应为偶数

2.曼哈顿距离：坐标系中两点  横坐标之差的绝对值+纵坐标的绝对值  之和

有何用处：预估最少步数，预估出来的步数一定是小于等于实际步数的

官方一点就是：求出初始矩阵与目标矩阵对应值得曼哈顿距离并求和（除去0）得到的值为评估值，写成函数即为评估函数。该值为从初始状态到目标状态所要经过的最小步数，实际步数只会大于等于该值。

算法介绍：

这次使用的算法是IDA*。我们首先是用逆序数进行判定是否有解，有解才进行搜索。有解的话，则先得到评估函数的初始值，该值为最小步数，递归深度（步数）必然大于等于这个初始值limit。我们先按深度搜索寻遍该深度的所有情况，看是否能找到解，有解则该解是最优解。若没解，则将深度的限制条件limit加1，再次递归下一层深度的所有情况，有解即为最优解，无解则继续将深度限制条件limit加1，这样不停循环直到某个深度maxLevel，则放弃寻找，因为在maxLevel步中没有找到，继续找下去时间花销太高，故放弃寻找。这就是IDA*中ID的意思，迭代加深。其中，算法在递归中使用了当前递归深度level,用level+评估函数(当前状态到目标状态至少需要的步数)<=limit作为剪枝条件，不满足该条件的在该分支上肯定无解。这样我们就可以找到在maxLevel步以内的最优解。

代码

//１５数码问题
#include<iostream>
#include<cstdlib>
#include<cmath>
#define size 4
using namespace std;

int move[][]={{-,},{,-},{,},{,}};//上,左,右,下增量
char op[]={'U','L','R','D'};
int map[size][size],map2[size*size],limit,path[];
//limit预估最少步数
int flag,length;
//int goal_st[3][3]={{1,2,3},{4,5,6},{7,8,0}};//目标状态
//goal存储目标位置，即０存在（３,３）,1存在（0,0）...
int goal[][]= {{,},{,},{,}, {,},
                  {,},{,},{,}, {,},
                  {,},{,},{,}, {,},
                  {,},{,},{,}, {,}};

int h(int a[size*size])//求逆序数 ，判断有无解
{
  int i,j,num,w,x,y; //w记录起点标号
  num=;  //逆序对数
  for(i=;i<size*size;i++)
  {
    if(a[i]==)
      w=i;
    for(j=i+;j<size*size;j++)
    {
      if(a[i]>a[j])
        num++;
    }
  }

  x=w/size;  //起点横坐标
  y=w%size;  //起点纵坐标 

  num+=abs(x-)+abs(y-);  //9102.9.7

  if(num%==)
    return ;
  else
    return ;
}

int manhattan(int a[][size])//计算曼哈顿距离，小等于实际总步数
{
  int i,j,cost=;
  for(i=;i<size;i++)
    for(j=;j<size;j++)
    {
      int w=map[i][j];
      cost+=abs(i-goal[w][])+abs(j-goal[w][]);
    }
  return cost;
}

void swap(int*a,int*b)
{
  int tmp;
  tmp=*a;
  *a=*b;
  *b=tmp;
}

void dfs(int sx,int sy,int dep,int pre_move)//sx,sy是空格的位置
{
  int i,j,nx,ny;
  if(flag)
    return;
  int dv=manhattan(map);
  if(dep==limit)
  {
    if(dv==)
    {
      flag=;
      length=dep;
      return;
    }
    else
      return;
  }
  else if(dep<limit)
  {
    if(dv==)
    {
      flag=;
      length=dep;
      return;
    }
  }
  for(i=;i<;i++)//４个方向尝试
  {
    if(i+pre_move==&&dep>)//不和上一次移动方向相反，对第二步以后而言
      continue;
    nx=sx+move[i][];
    ny=sy+move[i][];
    if(<=nx && nx<size && <=ny&&ny<size)//如果可以移动
    {
       swap(&map[sx][sy],&map[nx][ny]);//交换两位置
       int p=manhattan(map);
       if(p+dep<=limit&&!flag)
       {
          path[dep]=i;
         dfs(nx,ny,dep+,i);
         if(flag)
           return;
       }
       swap(&map[sx][sy],&map[nx][ny]);
    }
  }
}

int main()
{
  freopen("Puzzle15.in","r",stdin);
  freopen("Puzzle15.out","w",stdout);
  int i,j,k,l,m,n,sx,sy;
  char c,g;
  i=;
  scanf("%d",&n);
  while(n--)  //n组数据
  {
    flag=;length=;
    //flag判断有无解 

    memset(path,-,sizeof(path));
    //路径存储数组，记录每一步的抉择，也就是最后要输出的答案
    //（数字代码，后边转化成字符串） 

    for(i=;i<;i++)
    {
      scanf("%d",&map2[i]); //读入15数码图
      if(map2[i]==)  //寻找0在哪里
      {
        map[i/size][i%size]=;  //记录在图上的位置
        sx=i/size;sy=i%size;    //记录起点的横纵坐标
      }
      else
      {
        map[i/size][i%size]=map2[i];  //记录到图上
      }
    }

    if(h(map2)==)//该状态可达
    {
      limit=manhattan(map);
      while(!flag&&length<=)//题中要求50步之内到达
      {
        dfs(sx,sy,,);
        if(!flag)
          limit++; //得到的是最小步数
      }
      if(flag)
      {
        for(i=;i<length;i++)
          printf("%c",op[path[i]]);
        printf("\n");
      }
    }
    else if(!h(map2)||!flag)
      printf("This puzzle is not solvable.\n");
  }
  return ;
}

-----在崩溃的边缘疯狂试探-----