[COGS 755]山海经：线段树

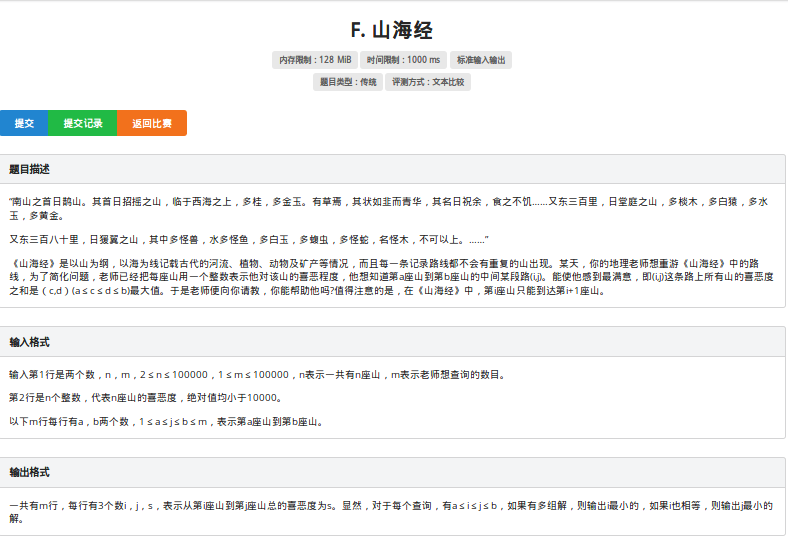
网上似乎这道题的题解很少？写一个吧

我跟这道题的渊源追溯到了上个学期刚刚学线段树的那一天。。。

当时线段树专题前边的题都是一些板子就不一会就水过了，然后就看到了最后一题的它：山海经

那一个上午，我竭尽全力，却毫无收获。

后来我下午继续肛还是肛不动，但是mikufun大神，在刚学线段树的阶段，把这道我现在都要写30min的难题给A了！

他当时的NB代码：

 #include<iostream>
 #include<cstdio>
 using namespace std;
 struct tree{
     int l,r,da,dam,dal,dar;
     int lme,lmr,le,lr;
 }t[];
 void build(int l1,int r1,int k){
     t[k].l=l1,t[k].r=r1;
     if(l1==r1){
         scanf("%d",&t[k].da);
         t[k].dal=t[k].dam=t[k].dar=t[k].da;
         t[k].le=t[k].lme=t[k].lmr=t[k].lr=l1;
         return;
     }
     int mid=(l1+r1)/;
     build(l1,mid,k*);
     build(mid+,r1,k*+);
     t[k].da=t[k*].da+t[k*+].da;
     if(t[k*].dal>=t[k*].da+t[k*+].dal){
         t[k].dal=t[k*].dal;
         t[k].le=t[k*].le;
     }
     else{
         t[k].dal=t[k*].da+t[k*+].dal;
         t[k].le=t[k*+].le;
     }
     if(t[k*+].dar>t[k*+].da+t[k*].dar){
         t[k].dar=t[k*+].dar;
         t[k].lr=t[k*+].lr;
     }
     else{
         t[k].dar=t[k*+].da+t[k*].dar;
         t[k].lr=t[k*].lr;
     }
     if(max(t[k*].dam,max(t[k*+].dam,t[k*].dar+t[k*+].dal))==t[k*].dam){
         t[k].dam=t[k*].dam;
         t[k].lme=t[k*].lme;t[k].lmr=t[k*].lmr;
     }
     else if(max(t[k*].dam,max(t[k*+].dam,t[k*].dar+t[k*+].dal))==t[k*+].dam){
         t[k].dam=t[k*+].dam;
         t[k].lme=t[k*+].lme;t[k].lmr=t[k*+].lmr;
     }
     else if(max(t[k*].dam,max(t[k*+].dam,t[k*].dar+t[k*+].dal))==t[k*].dar+t[k*+].dal){
         t[k].dam=t[k*].dar+t[k*+].dal;
         t[k].lme=t[k*].lr;t[k].lmr=t[k*+].le;
     }
 }
 inline int sea_qu(int l1,int r1,int k,int x,int &ll,int &rr){
     if(l1<=t[k].l&&t[k].r<=r1){
         if(!x){
             ll=t[k].lme;rr=t[k].lmr;
             return t[k].dam;
         }
         if(x==){
             ll=t[k].lr;rr=t[k].r;
             return t[k].dar;
         }
         if(x==){
             ll=t[k].l;rr=t[k].le;
             return t[k].dal;
         }
     }
     int mid=(t[k].l+t[k].r)/,ans,a1,a2,a3,a4,a5,a6;
     int a,b,c,d,e,g,h,z;
     if(x==){
         a1=sea_qu(l1,r1,k*+,,a,b);
         ll=a;rr=t[k].r;
         if(l1<=mid){
             a5=sea_qu(l1,r1,k*,,b,c)+t[k*+].da;
             if(a5>a1){
                 ll=b,rr=t[k].r;
                 return a5;
             }
         }
         return a1;
     }
     if(x==){
         a2=sea_qu(l1,r1,k*,,z,c);
         rr=c;ll=t[k].l;
         if(r1>mid){
             a6=sea_qu(l1,r1,k*+,,b,z)+t[k*].da;
             if(a6>a2){
                 ll=t[k].l,rr=z;
                 return a6;
             }
         }
         return a2;
     }
     if(!x){
         if(r1<=mid){
              ans=sea_qu(l1,r1,k*,,ll,rr);
              return ans;
         }
         if(l1>mid){
             ans=sea_qu(l1,r1,k*+,,ll,rr);
             return ans;
         }
         a1=sea_qu(l1,r1,k*,,a,b);
         a2=sea_qu(l1,r1,k*+,,b,c);
         a3=sea_qu(l1,r1,k*,,h,d);
         a4=sea_qu(l1,r1,k*+,,e,g);
          if(max(a1+a2,max(a3,a4))==a3){
              ll=h,rr=d;
              return a3;
         }
           if(max(a1+a2,max(a3,a4))==a1+a2){
             ll=a;
             rr=c;
             return a1+a2;
         }
         if(max(a1+a2,max(a3,a4))==a4){
             ll=e,rr=g;
             return a4;
         }
     }
 }
 int main(){
     int n,m,x,y,ll,rr;
     scanf("%d%d",&n,&m);
     build(,n,);
     for(int i=;i<=m;i++){
         scanf("%d%d",&x,&y);
         int ans=sea_qu(x,y,,,ll,rr);
         cout<<ll<<" "<<rr<<" "<<ans<<endl;
     }
     return ;
 }

这可是在当时，也就是没有题能打50行+的时候啊。

我当时看到有人A了都惊呆了。

我就去问mikufun，然后他说：“自己再想一想。”

我后来就一直想A掉这道题，可总有一些理由阻挡我蹒跚前进的脚步。

但现在我终于A了，很轻松释然。

我记得当时老吕看只有mikufunA了这道题，鼓励我们：“没事，只要知识没有丢，这些题你们以后看都很简单的。”

可是我当时想：“这么难的题，我恐怕一辈子都做不对了。”没想到啊，才几个月，变化已经这么大了。

OI改变你我。

题解：线段树维护左端点开始的最大值，右端点开始的最大值，区间最大值，以及它们的端点。

在子树合并到父亲时，父亲左端点开始的最大值可以由左儿子左端点开始的最大值，左儿子全部值+右左端点开始的最大值来更新。

同理于父亲右端点开始的最大值，区间最大值。但区间最大值还能够由左儿子右端点的最大值+右儿子左端点的最大值来更新。

总体上细节挺多的，注意好它字典序问题。其实就是几个顺序的调整罢了。

在merge合并时，我为了之后的查询更加方便，选择了用结构体进行合并，因为在find查找时由于[a,b]区间会被分成log个区间，因此等效于在子树合并到父亲。

 #include<bits/stdc++.h>
 #define N 100005
 #define Inf 0x7f7f7f7f
 #define lch k<<1
 #define rch k<<1|1
 inline int read(){
     int x=,f=;char ch=getchar();
     while(!isdigit(ch))f=(ch=='-'?-:),ch=getchar();
     while(isdigit(ch))x=x*+ch-'',ch=getchar();
     return x*f;
 }
 struct node{int l,r,mx,lmx,lp,rmx,rp,smx,slp,srp;}tr[N<<];
 int n,m;
 node merge(const node &t1,const node &t2){
     node ret;ret.lmx=ret.rmx=ret.smx=-Inf;
     ret.l=t1.l,ret.r=t2.r;ret.mx=t1.mx+t2.mx;
     ret.lmx=t1.lmx,ret.lp=t1.lp;
     ret.rmx=t2.rmx,ret.rp=t2.rp;
     if(t1.smx>=t2.smx) ret.smx=t1.smx,ret.slp=t1.slp,ret.srp=t1.srp;
     if(t1.rmx+t2.lmx>ret.smx) ret.smx=t1.rmx+t2.lmx,ret.slp=t1.rp,ret.srp=t2.lp;
     if(t1.rmx+t2.lmx==ret.smx&&( (t1.rp<ret.slp) || (t1.rp==ret.slp && t2.lp<ret.srp) )) ret.smx=t1.rmx+t2.lmx,ret.slp=t1.rp,ret.srp=t2.lp;
     if(t2.smx>ret.smx) ret.smx=t2.smx,ret.slp=t2.slp,ret.srp=t2.srp;
     if(t1.mx+t2.lmx>ret.lmx) ret.lmx=t1.mx+t2.lmx,ret.lp=t2.lp;
     if(t2.mx+t1.rmx>ret.rmx) ret.rmx=t2.mx+t1.rmx,ret.rp=t1.rp;
     if(ret.smx<=ret.lmx) ret.slp=ret.l,ret.srp=ret.lp;
     if(ret.smx<ret.rmx) ret.slp=ret.rp,ret.srp=ret.r;
     return ret;
 }
 void build(int k,int l,int r){
     tr[k].l=l,tr[k].r=r;
     if(l==r){tr[k].mx=tr[k].lmx=tr[k].rmx=tr[k].smx=read();tr[k].lp=tr[k].rp=tr[k].slp=tr[k].srp=l;return;}
     const int mid=(l+r)>>;
     build(lch,l,mid),build(rch,mid+,r);
     tr[k]=merge(tr[lch],tr[rch]);
 }
 node find(int k,int l,int r){
     if(tr[k].l>=l&&tr[k].r<=r) return tr[k];
     node ret;
     if(l<=tr[lch].r&&r>=tr[rch].l) ret=merge(find(lch,l,r),find(rch,l,r));
     else if(r<=tr[lch].r) ret=find(lch,l,r);
     else if(l>=tr[rch].l) ret=find(rch,l,r);
     return ret;
 }
 int main(){
     n=read(),m=read();
     build(,,n);
     int a,b;
     for(int i=;i<=m;++i){
         a=read(),b=read();
         node ret=find(,a,b);
         printf("%d %d %d\n",ret.slp,ret.srp,ret.smx);
     }
 }

我的超短超帅代码