模拟赛38 B. T形覆盖 大模拟
题目描述
如果玩过俄罗斯方块，应该见过如下图形：
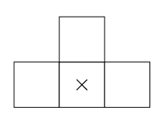
我们称它为一个 \(T\) 形四格拼板 。其中心被标记为\(×\)。
小苗画了一个 \(m\) 行 \(n\) 列的长方形网格。行从 \(0\) 至 \(m-1\) 编号，列从 \(0\) 至 \(n-1\) 编号。
她将网格中的一些格子标记为 特殊格子 。
然后，她想要她的朋友帮助她将 \(T\) 形四格拼板按找如下规则摆放：
\(1\)、 特殊格子的数量与 \(T\) 形四格拼板的数量相同，每个 \(T\) 形四格拼板的中心在网格上的位置必须是特殊格子。
\(2\)、 \(T\) 形四格拼板之间不能有重叠部分。
\(3\)、 所有拼板的部分均在网格内。
注意，\(T\) 形四格拼板有四种摆放方式：
如果方案不存在，输出 \(No\)，否则请找出一种方案使得被拼板覆盖的数总和最大，求出这个最大值。
输入格式
从文件 \(t-covering.in\) 中读入数据。
第一行两个整数 \(m,n\) 分别表示行数和列数。
接下来 \(m\) 行，每行 \(n\) 个整数，第 \(i\) 行第 \(j\) 个数（从 \(0\) 开始编号）表示方格中第 \(i\) 行第 \(j\) 列的数 \(a_{i,j}\)
接下来一行，一个整数 \(k\) ，表示特殊格子的数量。
接下来 \(k\) 行，每行两个整数 \(r_i,c_i\)，表示第 \(i\) 个被标记的特殊格子的位置。
输出格式
如果有方案，输出可能的被覆盖的格子内数总和的最大值，否则输出 \(No\)。
注意,本题 \(10\) 组测试数据均绑点, 只输出 \(1\) 个 \(No\) 不会得分.
样例
样例输入
5 6
7 3 8 1 0 9
4 6 2 5 8 3
1 9 7 3 9 5
2 6 8 4 5 7
3 8 2 7 3 6
3
1 1
2 2
3 4
样例输出
67
【样例 \(1\) 解释】
其中一种最优的方案如下：
\((1,1)\) 位置的摆放方式为 \(⊣\)。
\((2,2)\) 位置的摆放方式为\(⊢\)。
\((3,4)\) 位置的摆放方式为 \(⊥\)。
样例 \(2\) 输入
5 6
7 3 8 1 0 9
4 6 2 5 8 3
1 9 7 3 9 5
2 6 8 4 5 7
3 8 2 7 3 6
3
1 1
2 2
3 3
【样例 \(2\) 输出】
No
数据范围与提示
分析
把这道题打成了大模拟
思路是这样的：
\(1\)、把所有必须选的格子选上，这样的 \(T\) 有三种
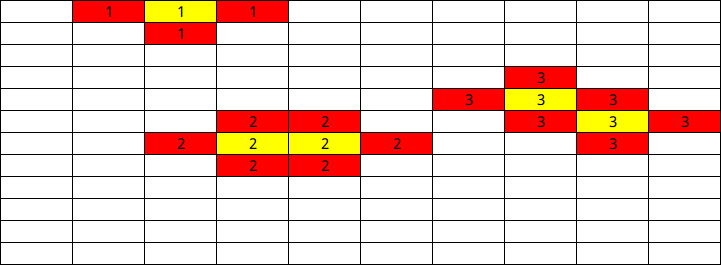
第一种是在边界上，第二种是两个格子直接相邻，第三种是两个格子对角线相邻
在没有限制的情况下，每一个 \(T\) 可以在周围的四个格子中任意选三个
而给了限制之后就只能选固定的三个了
要注意在选择过程中我们选择了一个格子后会使其它 \(T\) 能选择的格子减少
也就是说只能选择固定格子的 \(T\) 增加了，这个要存一下
\(2\)、对于两个 \(T\) 相隔一个格子的情况用并查集维护
把所有相隔一个格子的 \(T\)合并，如果形成的联通块没有环，可以贪心去掉一个最小的
如果有一个环，必须全部选上
如果有两个环即以上，则不合法
\(3\)、剩下的贪心去掉最小的即可
代码
#include<cstdio>
#include<vector>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<iostream>
#define rg register
inline int read(){
rg int x=0,fh=1;
rg char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') fh=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return x*fh;
}
const int maxn=1e6+5;
int n,m,k,cnt;
std::vector<int> a[maxn],id[maxn];
bool jud=0,vis[maxn],haha[maxn],inq[maxn],huan[maxn],s[maxn];
int tot[maxn],zxz[maxn],ans=0,js[maxn],sta[maxn],tp,jla[maxn],jlb[maxn];
struct asd{
int nx,ny;
asd(){}
asd(int aa,int bb){
nx=aa,ny=bb;
}
}b[maxn];
void xg(int nx,int ny){
if(nx<1 || ny<1 || nx>n || ny>m) return;
if(vis[id[nx][ny]]) return;
if(s[id[nx][ny]]==0) return;
js[id[nx][ny]]--;
if(!inq[id[nx][ny]]){
sta[++tp]=id[nx][ny];
inq[id[nx][ny]]=1;
}
}
int fa[maxn];
int zhao(int xx){
if(fa[xx]==xx) return xx;
return fa[xx]=zhao(fa[xx]);
}
int main(){
freopen("t_covering.in","r",stdin);
freopen("t_covering.out","w",stdout);
memset(zxz,0x3f,sizeof(zxz));
n=read(),m=read();
rg int aa,bb;
for(rg int i=1;i<=n;i++){
a[i].push_back(0);
id[i].push_back(0);
for(rg int j=1;j<=m;j++){
aa=read();
a[i].push_back(aa);
cnt++;
id[i].push_back(cnt);
}
}
k=read();
if(k*4>n*m){
printf("No\n");
for(rg int i=1;i<=k;i++){
aa=read(),bb=read();
}
return 0;
}
for(rg int i=1;i<=k;i++){
aa=read(),bb=read();
aa++,bb++;
if(s[id[aa][bb]]==1){
jud=1;
}
b[i].nx=aa,b[i].ny=bb;
jla[id[aa][bb]]=aa,jlb[id[aa][bb]]=bb;
s[id[aa][bb]]=1;
}
if(k){
if(n==1 || m==1) jud=1;
}
if(jud){
printf("No\n");
return 0;
}
for(rg int i=1;i<=k;i++){
js[id[b[i].nx][b[i].ny]]=4;
}
for(rg int i=1;i<=k;i++){
aa=b[i].nx,bb=b[i].ny;
if((aa==1 || aa==n) && (bb==1 || bb==m)){
printf("No\n");
return 0;
}
if(aa==1){
vis[id[aa][bb]]=1;
if(haha[id[aa][bb]] || haha[id[aa][bb-1]] || haha[id[aa][bb+1]] || haha[id[aa+1][bb]]){
printf("No\n");
return 0;
}
xg(aa,bb+2);
xg(aa,bb-2);
xg(aa+2,bb);
haha[id[aa][bb]]=haha[id[aa][bb-1]]=haha[id[aa][bb+1]]=haha[id[aa+1][bb]]=1;
ans+=a[aa][bb-1]+a[aa][bb+1]+a[aa+1][bb]+a[aa][bb];
} else if(aa==n){
vis[id[aa][bb]]=1;
if(haha[id[aa][bb]] || haha[id[aa][bb-1]] || haha[id[aa][bb+1]] || haha[id[aa-1][bb]]){
printf("No\n");
return 0;
}
xg(aa,bb+2);
xg(aa,bb-2);
xg(aa-2,bb);
haha[id[aa][bb]]=haha[id[aa][bb-1]]=haha[id[aa][bb+1]]=haha[id[aa-1][bb]]=1;
ans+=a[aa][bb-1]+a[aa][bb+1]+a[aa-1][bb]+a[aa][bb];
} else if(bb==1){
vis[id[aa][bb]]=1;
if(haha[id[aa][bb]] || haha[id[aa-1][bb]] || haha[id[aa+1][bb]] || haha[id[aa][bb+1]]){
printf("No\n");
return 0;
}
xg(aa-2,bb);
xg(aa+2,bb);
xg(aa,bb+2);
haha[id[aa][bb]]=haha[id[aa-1][bb]]=haha[id[aa+1][bb]]=haha[id[aa][bb+1]]=1;
ans+=a[aa-1][bb]+a[aa+1][bb]+a[aa][bb+1]+a[aa][bb];
} else if(bb==m){
vis[id[aa][bb]]=1;
if(haha[id[aa][bb]] || haha[id[aa-1][bb]] || haha[id[aa+1][bb]] || haha[id[aa][bb-1]]){
printf("No\n");
return 0;
}
xg(aa-2,bb);
xg(aa+2,bb);
xg(aa,bb-2);
haha[id[aa][bb]]=haha[id[aa-1][bb]]=haha[id[aa+1][bb]]=haha[id[aa][bb-1]]=1;
ans+=a[aa-1][bb]+a[aa+1][bb]+a[aa][bb-1]+a[aa][bb];
}
}
rg int mx,my;
for(rg int i=1;i<=k;i++){
aa=b[i].nx,bb=b[i].ny;
if(aa+1<=n){
mx=aa+1,my=bb;
if(s[id[mx][my]]){
if(!vis[id[mx][my]]){
vis[id[mx][my]]=1;
if(haha[id[mx][my+1]] || haha[id[mx][my-1]] || haha[id[mx+1][my]] || haha[id[mx][my]]){
printf("No\n");
return 0;
}
xg(mx,my+2);
xg(mx,my-2);
xg(mx+2,my);
haha[id[mx][my+1]]=haha[id[mx][my-1]]=haha[id[mx+1][my]]=haha[id[mx][my]]=1;
ans+=a[mx][my+1]+a[mx][my-1]+a[mx+1][my]+a[mx][my];
}
if(!vis[id[aa][bb]]){
vis[id[aa][bb]]=1;
if(haha[id[aa][bb-1]] || haha[id[aa][bb+1]] || haha[id[aa-1][bb]] || haha[id[aa][bb]]){
printf("No\n");
return 0;
}
xg(aa,bb-2);
xg(aa,bb+2);
xg(aa-2,bb);
haha[id[aa][bb-1]]=haha[id[aa][bb+1]]=haha[id[aa-1][bb]]=haha[id[aa][bb]]=1;
ans+=a[aa][bb-1]+a[aa][bb+1]+a[aa-1][bb]+a[aa][bb];
vis[id[aa][bb]]=1;
}
}
}
if(bb+1<=m){
mx=aa,my=bb+1;
if(s[id[mx][my]]){
if(!vis[id[mx][my]]){
vis[id[mx][my]]=1;
if(haha[id[mx+1][my]] || haha[id[mx-1][my]] || haha[id[mx][my+1]] || haha[id[mx][my]]){
printf("No\n");
return 0;
}
xg(mx-2,my);
xg(mx+2,my);
xg(mx,my+2);
haha[id[mx+1][my]]=haha[id[mx-1][my]]=haha[id[mx][my+1]]=haha[id[mx][my]]=1;
ans+=a[mx+1][my]+a[mx-1][my]+a[mx][my+1]+a[mx][my];
}
if(!vis[id[aa][bb]]){
vis[id[aa][bb]]=1;
if(haha[id[aa-1][bb]] || haha[id[aa+1][bb]] || haha[id[aa][bb-1]] || haha[id[aa][bb]]){
printf("No\n");
return 0;
}
xg(aa-2,bb);
xg(aa+2,bb);
xg(aa,bb-2);
haha[id[aa-1][bb]]=haha[id[aa+1][bb]]=haha[id[aa][bb-1]]=haha[id[aa][bb]]=1;
ans+=a[aa-1][bb]+a[aa+1][bb]+a[aa][bb-1]+a[aa][bb];
vis[id[aa][bb]]=1;
}
}
}
}
for(rg int i=1;i<=k;i++){
aa=b[i].nx,bb=b[i].ny;
if(aa+1<=n && bb+1<=m){
mx=aa+1,my=bb+1;
if(s[id[mx][my]]){
if(!vis[id[mx][my]]){
vis[id[mx][my]]=1;
if(haha[id[mx+1][my]] || haha[id[mx-1][my]] || haha[id[mx][my+1]] || haha[id[mx][my]]){
printf("No\n");
return 0;
}
xg(mx-2,my);
xg(mx+2,my);
xg(mx,my+2);
haha[id[mx+1][my]]=haha[id[mx-1][my]]=haha[id[mx][my+1]]=haha[id[mx][my]]=1;
ans+=a[mx+1][my]+a[mx-1][my]+a[mx][my+1]+a[mx][my];
}
if(!vis[id[aa][bb]]){
vis[id[aa][bb]]=1;
if(haha[id[aa+1][bb]] || haha[id[aa-1][bb]] || haha[id[aa][bb-1]] || haha[id[aa][bb]]){
printf("No\n");
return 0;
}
xg(aa-2,bb);
xg(aa+2,bb);
xg(aa,bb-2);
haha[id[aa+1][bb]]=haha[id[aa-1][bb]]=haha[id[aa][bb-1]]=haha[id[aa][bb]]=1;
ans+=a[aa+1][bb]+a[aa-1][bb]+a[aa][bb-1]+a[aa][bb];
vis[id[aa][bb]]=1;
}
}
}
if(bb-1>=1 && aa+1<=n){
mx=aa+1,my=bb-1;
if(s[id[mx][my]]){
if(!vis[id[mx][my]]){
vis[id[mx][my]]=1;
if(haha[id[mx+1][my]] || haha[id[mx-1][my]] || haha[id[mx][my-1]] || haha[id[mx][my]]){
printf("No\n");
return 0;
}
xg(mx-2,my);
xg(mx+2,my);
xg(mx,my-2);
haha[id[mx+1][my]]=haha[id[mx-1][my]]=haha[id[mx][my-1]]=haha[id[mx][my]]=1;
ans+=a[mx+1][my]+a[mx-1][my]+a[mx][my-1]+a[mx][my];
}
if(!vis[id[aa][bb]]){
vis[id[aa][bb]]=1;
if(haha[id[aa+1][bb]] || haha[id[aa-1][bb]] || haha[id[aa][bb+1]] || haha[id[aa][bb]]){
printf("No\n");
return 0;
}
xg(aa-2,bb);
xg(aa+2,bb);
xg(aa,bb+2);
haha[id[aa+1][bb]]=haha[id[aa-1][bb]]=haha[id[aa][bb+1]]=haha[id[aa][bb]]=1;
ans+=a[aa+1][bb]+a[aa-1][bb]+a[aa][bb+1]+a[aa][bb];
vis[id[aa][bb]]=1;
}
}
}
}
for(rg int i=1;i<=tp;i++){
if(vis[sta[i]]) continue;
if(js[sta[i]]<=2){
printf("No\n");
return 0;
} else {
mx=jla[sta[i]],my=jlb[sta[i]];
ans+=a[mx][my+1]+a[mx][my-1]+a[mx+1][my]+a[mx-1][my]+a[mx][my];
vis[sta[i]]=1;
if(haha[id[mx][my+1]]){
ans-=a[mx][my+1];
xg(mx-2,my);
xg(mx+2,my);
xg(mx,my-2);
} else if(haha[id[mx][my-1]]){
ans-=a[mx][my-1];
xg(mx-2,my);
xg(mx+2,my);
xg(mx,my+2);
} else if(haha[id[mx-1][my]]){
ans-=a[mx-1][my];
xg(mx,my-2);
xg(mx,my+2);
xg(mx+2,my);
} else {
ans-=a[mx+1][my];
xg(mx,my-2);
xg(mx,my+2);
xg(mx-2,my);
}
}
}
for(rg int i=1;i<=cnt;i++){
fa[i]=i;
}
rg int cc,dd;
for(rg int i=1;i<=k;i++){
if(vis[id[b[i].nx][b[i].ny]]) continue;
aa=b[i].nx,bb=b[i].ny;
cc=id[b[i].nx][b[i].ny];
tot[cc]+=a[aa][bb]+a[aa-1][bb]+a[aa+1][bb]+a[aa][bb-1]+a[aa][bb+1];
zxz[cc]=std::min(std::min(a[aa+1][bb],a[aa-1][bb]),std::min(a[aa][bb-1],a[aa][bb+1]));
}
for(rg int i=1;i<=k;i++){
if(vis[id[b[i].nx][b[i].ny]]) continue;
aa=b[i].nx,bb=b[i].ny;
mx=b[i].nx+2,my=b[i].ny;
if(mx<=n && s[id[mx][my]]){
cc=zhao(id[aa][bb]),dd=zhao(id[mx][my]);
if(cc==dd){
if(huan[cc]){
printf("No\n");
return 0;
}
huan[cc]=1;
tot[cc]-=a[aa+1][bb];
zxz[cc]=0;
} else {
tot[cc]+=tot[dd];
tot[cc]-=a[aa+1][bb];
zxz[cc]=std::min(zxz[cc],zxz[dd]);
fa[dd]=cc;
}
}
mx=b[i].nx,my=b[i].ny+2;
if(my<=m && s[id[mx][my]]){
cc=zhao(id[aa][bb]),dd=zhao(id[mx][my]);
if(cc==dd){
if(huan[cc]){
printf("No\n");
return 0;
}
huan[cc]=1;
tot[cc]-=a[aa][bb+1];
zxz[cc]=0;
} else {
tot[cc]+=tot[dd];
tot[cc]-=a[aa][bb+1];
zxz[cc]=std::min(zxz[cc],zxz[dd]);
fa[dd]=cc;
}
}
}
for(rg int i=1;i<=k;i++){
if(vis[id[b[i].nx][b[i].ny]]) continue;
mx=b[i].nx,my=b[i].ny;
if(fa[id[mx][my]]!=id[mx][my]) continue;
ans+=tot[id[mx][my]]-zxz[id[mx][my]];
}
printf("%d\n",ans);
return 0;
}
模拟赛38 B. T形覆盖 大模拟的更多相关文章
- noip模拟赛#38
我打开了#39的problem...想了半个小时多发现我一道题都不会写...于是我打开了#38的problem T1:循环数字的定义为能够将该数划分为若干相同长度的段并且都相同. n=2e18. =& ...
- [luogu#2019/03/10模拟赛][LnOI2019]长脖子鹿省选模拟赛赛后总结
t1-快速多项式变换(FPT) 题解 看到这个\(f(x)=a_0+a_1x+a_2x^2+a_3x^3+ \cdots + a_nx^n\)式子,我们会想到我们学习进制转换中学到的,那么我们就只需要 ...
- [模拟赛FJOI Easy Round #2][T1 sign] (模拟+求字符串重复字串)
[题目描述] 小Z在无意中发现了一个神奇的OJ,这个OJ有一个神奇的功能:每日签到,并且会通过某种玄学的算法计算出今日的运势.在多次试验之后,小Z发现自己的运势按照一定的周期循环,现在他找到了你,请通 ...
- 模拟赛小结：2017-2018 ACM-ICPC Nordic Collegiate Programming Contest (NCPC 2017)
比赛链接:传送门 本场我们队过的题感觉算法都挺简单的,不知道为啥做的时候感觉没有很顺利. 封榜后7题,罚时1015.第一次模拟赛金,虽然是北欧的区域赛,但还是有点开心的. Problem B Best ...
- 【2020.8.23NOIP模拟赛】失落
[ 2020.8.23 N O I P 模 拟 赛 ] 失 落 [2020.8.23NOIP模拟赛]失落 [2020.8.23NOIP模拟赛]失落 题目描述 出题人心情很失落,于是他直接告诉你让你求出 ...
- HDU 5920 Ugly Problem 高精度减法大模拟 ---2016CCPC长春区域现场赛
题目链接 题意:给定一个很大的数,把他们分为数个回文数的和,分的个数不超过50个,输出个数并输出每个数,special judge. 题解:现场赛的时候很快想出来了思路,把这个数从中间分为两部分,当位 ...
- 2016ACM-ICPC网络赛北京赛区 1001 （trie树牌大模拟）
[题目传送门] 1383 : The Book List 时间限制:1000ms 单点时限:1000ms 内存限制:256MB 描述 The history of Peking University ...
- 体育成绩统计——20180801模拟赛T3
体育成绩统计 / Score 题目描述 正所谓“无体育,不清华”.为了更好地督促同学们进行体育锻炼,更加科学地对同学们进行评价,五道口体校的老师们在体育成绩的考核上可谓是煞费苦心.然而每到学期期末时, ...
- [GRYZ]寒假模拟赛
写在前面 这是首次广饶一中的OIERS自编自导,自出自做(zuo)的模拟赛. 鉴于水平气压比较低,机(wei)智(suo)的WMY/XYD/HYXZC就上网FQ下海找了不少水(fei)题,经过他们优( ...
随机推荐
- java面试之手写单例模式
为什么要有单例模式 实际编程应用场景中,有一些对象其实我们只需要一个,比如线程池对象.缓存.系统全局配置对象等.这样可以就保证一个在全局使用的类不被频繁地创建与销毁,节省系统资源. 实现单例模式的几个 ...
- 学会Git玩转GitHub(第二篇) 入门详解 - 精简归纳
学会Git玩转GitHub(第二篇) 入门详解 - 精简归纳 JERRY_Z. ~ 2020 / 10 / 25 转载请注明出处!️ 目录 学会Git玩转GitHub(第二篇) 入门详解 - 精简归纳 ...
- Docker指令整理
date: 2018-11-18 11:09:28 updated: 2018-11-18 11:09:28 Docker指令整理 管理员权限!!! 查看docker版本 docker -v 启动 s ...
- Tomcat8升级后URL中特殊字符报错出现原因
请求带上花括号等字符,请求无法送达服务端,报错: Failed to load resource: the server responded with a status of 400 () https ...
- Jetson AGX Xavier ROS下调用USB单目摄像头
Jetson AGX Xavier安装的ROS是Melodic版本的,所以部署的时候用到的包都是Melodic的. 1. 查看USB摄像头 摄像头连接Xavier设备,调用命令查看. ls /dev/ ...
- Map 和 Json 互转
Json 转 Map<String,String> String query = "{tableName:\"iov_biz_car_info\",selec ...
- Luogu P3846 [TJOI2007] 可爱的质数/【模板】BSGS
题意 给定 \(y,z,p\),求最小的正整数 \(x\) 满足 \(y^x\equiv z\bmod p\),保证 \(p\) 是质数. \(\texttt{Data Range:}2\leq y, ...
- NB-IOT基站的优势和特点
NB-IOT基站是什么 NB-IOT基站的主要目的是完成移动通信网和UE之间的通信和管理功能,在移动通信中是组成蜂窝小区最基本的单元.只有在基站信号的覆盖范围之内通过运营商网络连接的NB ...
- 浅谈 Tarjan 算法
目录 简述 作用 Tarjan 算法 原理 出场人物 图示 代码实现 例题 例题一 例题二 例题三 例题四 例题五 总结 简述 对于初学 Tarjan 的你来说,肯定和我一开始学 Tarjan 一样无 ...
- dhcp、tftp、httpd、pxe安装CentOS6.9
虚拟机网络设置 要xshell连接虚拟机注意设置VMware Network Adapter VMnet2在同一网段 1.利用光盘配置本地yum源 [root@ZYB ~]# mount -r /de ...