exkmp（Z函数） 笔记

exkmp 用于求解这样的问题：

求文本串 \(T\) 的每一个后缀与模式串 \(M\) 的匹配长度（即最长公共前缀长度）。特别的，取 \(M=T\)，得到的这个长度被称为 \(Z\) 函数。“函数”只是一个叫法，它本质上是个数组...为了好听，后面叫他“\(Z\) 数组” （互联网上的确有人这么叫）

符号(字符串)

\(|S|\) 表示 \(S\) 的长度

\(S[l:r]\) 表示 \(S\) 从 \(l\) 到 \(r\) 的子串。如果 \(l\) 空着，默认为 \(1\)；同理 \(r\) 默认为 \(|S|\)。

也就是 \(S[:x]\) 表示 \(S\) 到 \(x\) 结束的前缀，\(S[x:]\) 表示 \(S\) 从 \(x\) 开始的后缀。

\(LCP(S_1,S_2)\) 表示 \(S_1,S_2\) 的 最长公共前缀 （Longest Common Prefix）

算法讲解

设 \(p_i=LCP(T_i,M)\)

定义从 \(l\) 开始的匹配区间为 \([l,l+p_l-1]\) （设 \(l+p_l-1=r\)）

我们枚举处理。假设现在已经求好了 \([1,i-1]\) 的 \(p\) 数组，要求 \(p_i\)。记录一个 最靠后 的匹配区间 \([l,r]\) （\(l<i\)，以 \(r\) 靠后为第一关键字，\(l\) 靠后为第二关键字），考虑直接从 \([l,r]\) 中继承点答案来，那很显然一个前提就是 \(i\le r\) （你 \(i\) 在 \(r\) 外面继承啥）

显然，\(p_i\ge LCP(T[i:r],M)\) （因为 \(T[i:r]\) 是 \(T[i:]\) 前缀）

由定义， \([l,r]\) 是最长匹配长度，可知 \(T[l:r]=M[1:r-l+1]\)。

然后现在假如 \(l<i\le r\)，那么显然 \(T[i:r]=M[i-l+1:r-l+1]\)

那么 \(LCP(T[i:r],M)=LCP(M[i-l+1:r-l+1],M)\)

简单想一下，\(LCP(A[l:r],A)=min(LCP(A[l:],A),r-l+1)\)

我们要求 \([l,r]\) 子串与整个串的 \(LCP\)，可以先求以 \(l\) 开头的整个后缀的与整个串的 \(LCP\)，然后和区间长度取 \(min\)。这显然正确。

然后有：

\(LCP(M[i-l+1:r-l+1],M)=min(LCP(M[i-l+1:],M),(r-l+1)-(i-l+1+1))\)

右边的 \(-l+1\) 两个抵消了，就变成 \(r-i+1\)

然后前面是 \(LCP(M[i-l+1:],M)\) 。这不就是 \(M\) 的 \(Z\) 数组的第 \(i-l+1\) 个位置吗！（还记得 \(Z\) 数组的定义吗？）

觉得看字母理解不了的看图（自己画的）（纯鼠标）：

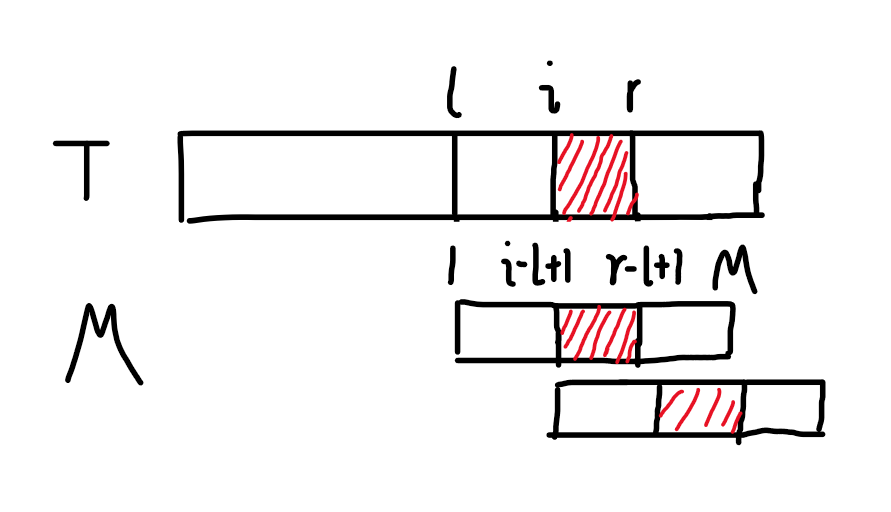
红色的部分就是我们推出来的匹配部分。然后现在我们把 \(M\) 移到 \(i\) 开头的位置来匹配，就相当于把 \(M[i-l+1:r-l+1]\) 这一段（红色）移到 \(M\) 的开头处匹配。这一段匹配的长度就是 \(min(Z_{i-l+1},r-i+1)\)。

假设我们现在能求这个 \(Z\) 数组，那么我们已经知道 \(p_i\) 的最小值了 ，就是 \(min(Z_{i-l+1},r-i+1)\) 。从这个位置开始暴力即可。这样就不用每次从 \(1\) 开始匹配了。

求完 \(p_i\) 之后，记得用 \([i,i+p_i-1]\) 更新 \([l,r]\)。

update 2021.01.20:

时间是线性的。原因是，每次成功匹配之后，能直接继承答案的区间便多了一位，复杂度便是线性的。

证明由神仙学长 tzxydby 提供

如何求 Z 数组

我们发现 \(Z\) 数组就是自己和自己匹配的过程。然后我们把上面过程中 \(M\) 换成 \(T\) 即可。

所以我们还是记录一个最靠后的匹配区间 \([l,r]\)，然后 \(p_i\) 就相当于 \(Z_i\) 了。

易得：

\(Z_i=min(LCP(M[i-l+1:],M),r-i+1)=min(LCP(T[i-l+1:],T),r-i+1)=min(Z_{i-l+1},r-i+1)\)

求完 \(Z_i\) 之后，记得用 \([i,i+Z_i-1]\) 来更新 \([l,r]\)。

一样，也是从这里开始暴力即可。同理，时间复杂度依然是线性的。

模板

洛谷板子

#include <bits/stdc++.h>
using namespace std;
#define N 20000007
#define F(i,l,r) for(int i=l;i<=r;++i)
#define D(i,r,l) for(int i=r;i>=l;--i)
#define Fs(i,l,r,c) for(int i=l;i<=r;c)
#define Ds(i,r,l,c) for(int i=r;i>=l;c)
#define MEM(x,a) memset(x,a,sizeof(x))
#define FK(x) MEM(x,0)
#define Tra(i,u) for(int i=G.Start(u),v=G.To(i);~i;i=G.Next(i),v=G.To(i))
#define p_b push_back
#define sz(a) ((int)a.size())
#define all(a) a.begin(),a.end()
#define iter(a,p) (a.begin()+p)
#define Flandre_Scarlet int
#define IsMyWife main
char _c;
int I()
{
    int x=0; int f=1;
    while(_c<'0' or _c>'9') f=(_c=='-')?-1:1,_c=getchar();
    while(_c>='0' and _c<='9') x=(x<<1)+(x<<3)+(_c^48),_c=getchar();
    return (x=(f==1)?x:-x);
}
void Rd(int cnt,...)
{
    va_list args; va_start(args,cnt);
    F(i,1,cnt) {int* x=va_arg(args,int*);(*x)=I();}
    va_end(args);
}

char a[N],b[N];
void Input()
{
	scanf("%s%s",a+1,b+1);
}
int z[N];
void Z(char s[]) // 求 Z 函数
{
	int n=strlen(s+1);
	z[1]=n; F(i,2,n) z[i]=0;
    // Z[1]=n 特判，同时也是递推边界
	int l=0,r=0;
	F(i,2,n)
	{
		if (i<=r) z[i]=min(z[i-l+1],r-i+1); // 推理出下界
		while(i+z[i]<=n and s[i+z[i]]==s[z[i]+1]) ++z[i]; // 暴力
		if (i+z[i]-1>=r) l=i,r=i+z[i]-1; // 更新最靠后的匹配位置
	}
}
int p[N];
void ExKmp(char s[],char t[])
{
	int n=strlen(s+1);
	Z(t);
	int l=0,r=0;
	F(i,1,n)
	{
		if (i<=r) p[i]=min(z[i-l+1],r-i+1); // 推理出下界
		while(i+p[i]<=n and s[i+p[i]]==t[p[i]+1]) ++p[i]; // 暴力
		if (i+p[i]-1>r) l=i,r=i+p[i]-1; // 更新最靠后的匹配位置
	}
}
void Soviet()
{
	ExKmp(a,b);
	int n=strlen(a+1),m=strlen(b+1);
	long long ans=0;
	F(i,1,m) ans^=1ll*i*(z[i]+1);
	printf("%lld\n",ans);
	ans=0;
	F(i,1,n) ans^=1ll*i*(p[i]+1);
	printf("%lld\n",ans);
}
Flandre_Scarlet IsMyWife()
{
	Input();
	Soviet();
	getchar();
	return 0;
}