CF1693D--单调区间

\(T_4\) 单调区间结题报告

题目描述

一句话题意：给定一个排列 \(a\) 算出有多少个区间 \([l , r]\) , 满足其可以划分为一个单调递增子序列和单调递减子序列，其中单调递增子序列长度 \(\ge 1\) , 单调递减子序列长度可为 \(0\) . \(n \le 10 ^ 5\)

题解

呃呃能自己想出来挺不容易的，废了老子一下午一晚上。

感觉大家在证分治做法的复杂度，我也不淌这潭浑水了，本做法为 \(n \log n\) , 使用树状数组和优先队列数据结构。

首先考虑一个结论，对于一个不满足条件的区间 \([a , b]\) ，其一定满足如下条件:

对于 \(a \le i < j < k < l \le b\) , 满足:

\[a_k < a_l < a_i < a_j \ \lor \ a_j < a_i < a_l < a_k \ \ \ \ \ \ \ \ \ \ \ (1)
\]

手模一下就能发现这样构成不了合法解。

两个图:(图是反的)

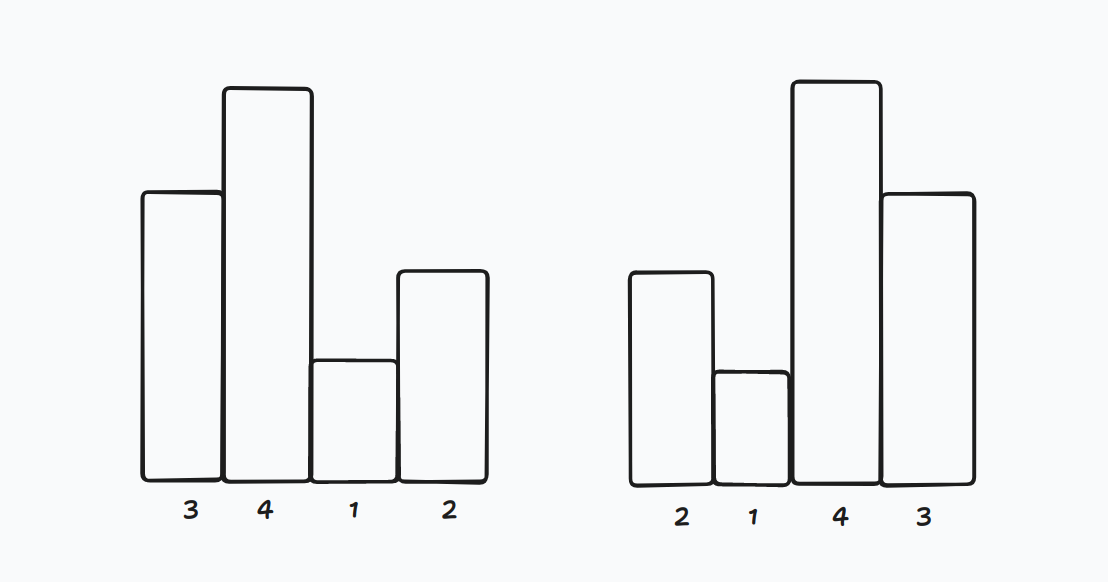
我们又发现假设我们目前为 \(l\) , 那么对于上面的结论来说，去找最大满足上述结论的 \(\max\{i\}\) .

那么 \(l\) 贡献出的答案为 $$l - \max{i}$$

当然，我们称 \(\max\{i\}\) 为 \(l\) 的左端点 \(L_l\)

对于 \(\alpha < l\) , 那么 \([i , l] \ \left(i \le L_{\alpha}\right)\) 区间同样取不到。

于是得到进阶结论:

对于排列 \(a\) : ( \(L\) 定义不变 )

\[ans = \sum_{i = 1}^{n} i - \max_{1 \le j \le i}\{L_j\} \ \ \ \ \ \ \ \ \ \ (2)
\]

然后我们考虑去求 \(L_i\)

我们对于结论 \(1\) 来说，可以分成或左或右两方分讨。

对于一种情况来说 (假设为第一种) ， 设目前为 \(d\) .

让目前那四个数为 \(a , b , c , d\)

一个显然的结论:

我们如果为了让 \(L_d\) 最小，\(c\) 一定是离 \(d\) 最近，且 \(a_c > a_d\) 的点。

贪心显然

于是我们可以去枚举 \(c\) , 以 \(c\) 为下标存储 \(d\) .

那我们求 \(L_d\) 时 , 显然是某个 \(1 \le i < c\) ， 且 \(i\) 满足 \(a_i < a_d \ \land \ \exists \ j : i < j < c , a_j < a_i\) .

其实无脑一下就是上图中(后面的图) 最后一个大于第一个，第一个大于第二个，找下标最大的第一个。

所以可以开一个树状数组，就是以 \(a_i\) 为下标，维护 \(i\) .

(有人有疑惑为什么不从图中第二个位置转移吗? 那样看起来还好处理一点)

错误点在于第二个点要从比他大的转移来，然而比他大的怎么就一定比 \(a_d\) 小呢？

例子： \(3 , 100 , 2 , 1000 , 5\)

如果你从 你按你的想法查 \(2\) , 查出来的位置是 \(2\) . 不合法。

因此需要算，如果存在一个比 \(a_i\) 小的数刚刚加进来，就可以把 \(i\) ，扔进树状数组了。

具体可以用一个大根堆，在枚举 \(c\) ，并处理完 \(d\) 后，将所有在优先队列中大于 \(a_c\) 的数加进树状数组(此时的 \(c\) 就是后面某次的 \(b\) 啊!) 差的时候查 \([1 , a_i)\) 中下标最大值 (显然是插进树状数组中的的才可以转移)。

对于第一个图，处理差不多，不再赘述。

然而就是说第一个图，要求 \(\max\limits_{i < j \le n}\{val_j\}\)

( \(val\) 是树状数组维护的值 )

即后缀和。我们只需要把输转数组反过来存， \(n - i + 1\) 存 \(i\) .

\(Code\)

CODE

#include <bits/stdc++.h>
#include <bits/extc++.h>
#define int long long
#ifdef linux
#define getchar getchar_unlocked
#endif
using namespace std ;
using namespace __gnu_pbds ;
using namespace __gnu_cxx ;
typedef long long ll ;
const int N = 4e5 + 100 ;
inline int read() {
	int x = 0 , f = 1 ;
	char c = getchar() ; 

	while (c < '0' || c > '9') {
		if (c == '-') f = -f ; 

		c = getchar() ;
	}

	while (c >= '0' && c <= '9') {
		x = x * 10 + c - '0' ;
		c = getchar() ;
	}

	return x * f ;
}

int n ; int a[N] ; int Ans[N] ; 

struct Binary_Index_Array_Max {
	#define lowbit(x) (x & (- x))
	int t[N] ; 

	void clear() {
		memset(t , 0 , sizeof(t)) ;
	}

	void add(int pos , int val) {
		while (pos <= n) {
			t[pos] = max(t[pos] , val) ;
			pos += lowbit(pos) ;
		}
	}

	int Query(int pos) {
		int ans = 0 ; 

		while (pos > 0) {
			ans = max(t[pos] , ans) ;
			pos -= lowbit(pos) ;
		}

		return ans ;
	}
} t1 , t2 ; 

int front1[N] , front2[N] ;
vector <int> v1[N] , v2[N] ;
__gnu_pbds :: priority_queue <int , less<int> > q1 ;
__gnu_pbds :: priority_queue <int , greater<int> > q2 ; 

int pos[N] ; 

signed main() {
	n = read() ;
	for (int i = 1 ; i <= n ; ++ i) a[i] = read() , pos[a[i]] = i ;
	for (int i = 1 ; i <= n ; ++ i) {
		front1[i] = t1.Query(n - a[i] + 1) ; v1[front1[i]].push_back(i) ;
		front2[i] = t2.Query(a[i]) ; v2[front2[i]].push_back(i) ;
		t1.add(n - a[i] + 1 , i) ; t2.add(a[i] , i) ;
	} t1.clear() ; 

	for (int i = 1 ; i <= n ; ++ i) {
		for (auto j : v1[i]) {
			Ans[j] = t1.Query(a[j] - 1) ;
		}

		while (!q1.empty()) {
			int x = q1.top() ;
			if (x <= a[i]) break ; q1.pop() ;
			t1.add(x , pos[x]) ;
		} q1.push(a[i]) ;
	} t1.clear() ; 

	for (int i = 1 ; i <= n ; ++ i) {
		for (auto j : v2[i]) {
			Ans[j] = max(Ans[j] , t1.Query(n - (a[j] + 1) + 1)) ;
		}

		while (!q2.empty()) {
			int x = q2.top() ;
			if (x >= a[i]) break ; q2.pop() ;
			t1.add(n - x + 1 , pos[x]) ;
		} q2.push(a[i]) ;
	}

	int Ansp = 0 ; 

	for (int i = 1 ; i <= n ; ++ i) {
		Ans[i] = max(Ans[i] , Ans[i - 1]) ;
		Ansp += i - Ans[i] ;
	}

	cout << Ansp << '\n' ;
}