二叉树的 Morris 中序遍历——O(1)空间复杂度

回顾

问题陈述： 给定一棵二叉树，实现中序遍历并返回包含其中序序列的数组

例如给定下列二叉树：



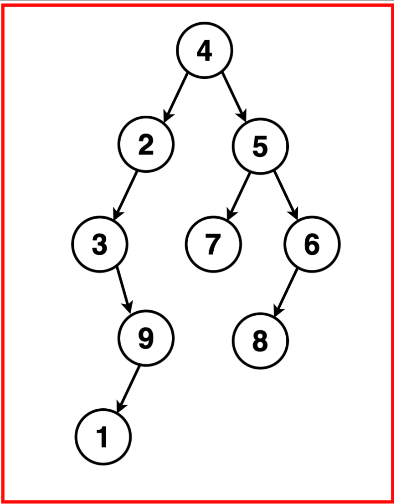
我们按照左、根、右的顺序递归遍历二叉树，得到以下遍历：



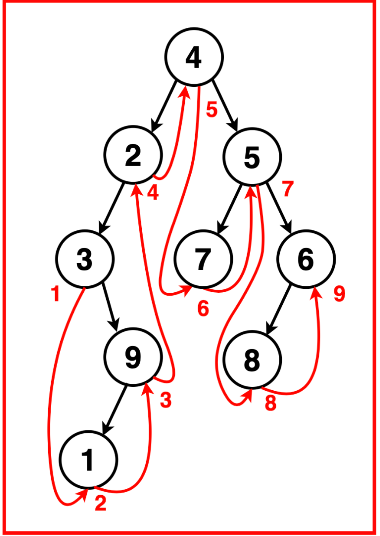
最终中序遍历结果可以输出为： [3, 1, 9, 2, 4, 7, 5, 8, 6]

Morris trick

Morris 中序遍历是一种树遍历算法，旨在实现 O(1) 的空间复杂度，无需递归或外部数据结构。该算法应高效地按中序顺序访问二叉树中的每个节点，并在遍历过程中打印或处理节点值，而无需使用堆栈或递归。

关键思想是在 current node 与其对应的 rightmost node 之间建立临时链接

先来看下中序遍历的过程：

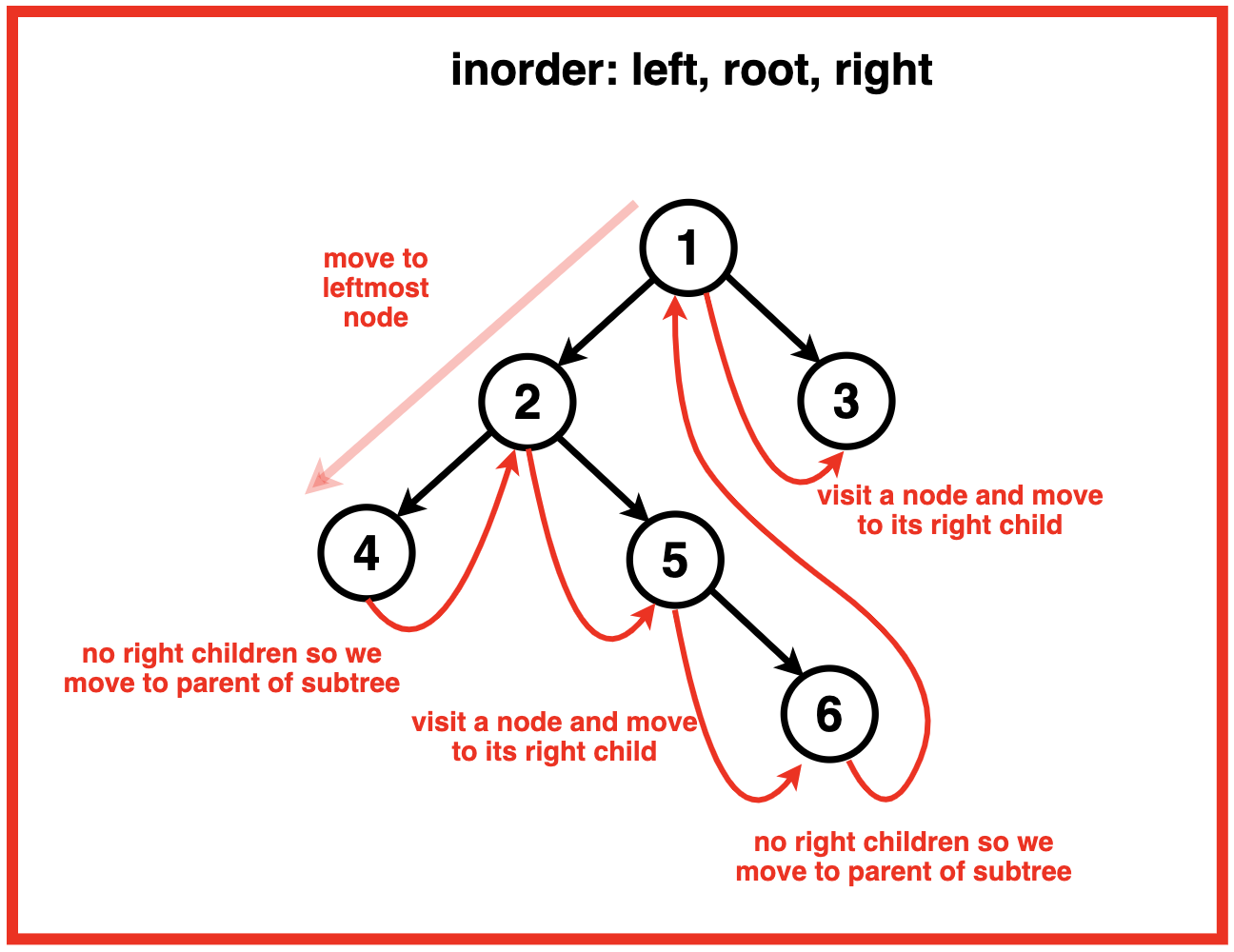
做法讨论

节点的中序前驱是左子树中最右边的节点。因此，当我们遍历左子树时，我们会遇到一个右子节点为空的节点，这是该子树中的最后一个节点。因此，我们观察到一种模式，每当我们处于子树的最后一个节点时，如果右子节点指向空，我们就会移动到该子树的父节点。

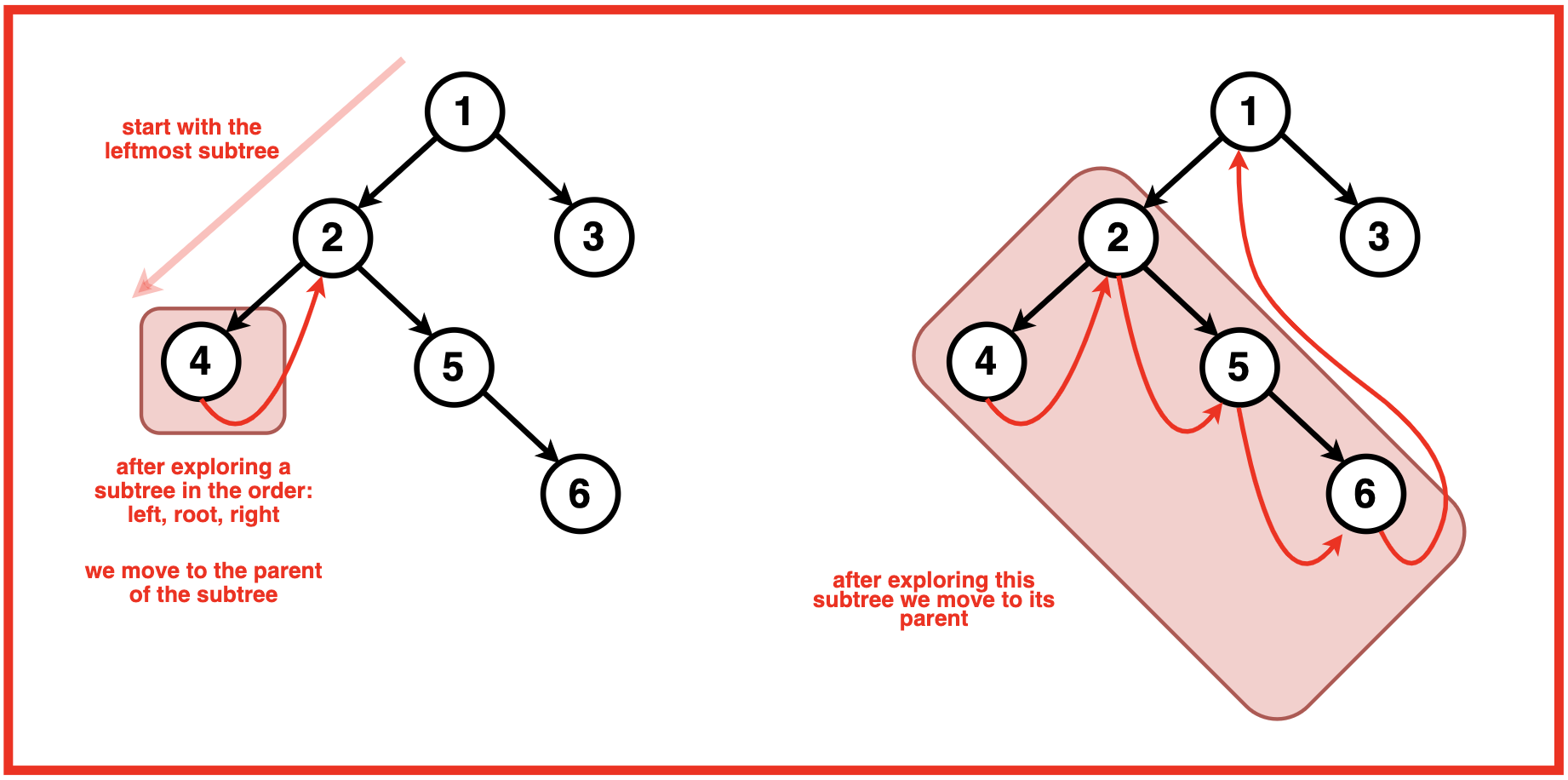
当我们当前处于某个节点时，可能会出现以下情况：

情况1：当前节点没有左子树

• 打印当前节点的值
• 然后到当前节点的右子节点
  
  
  
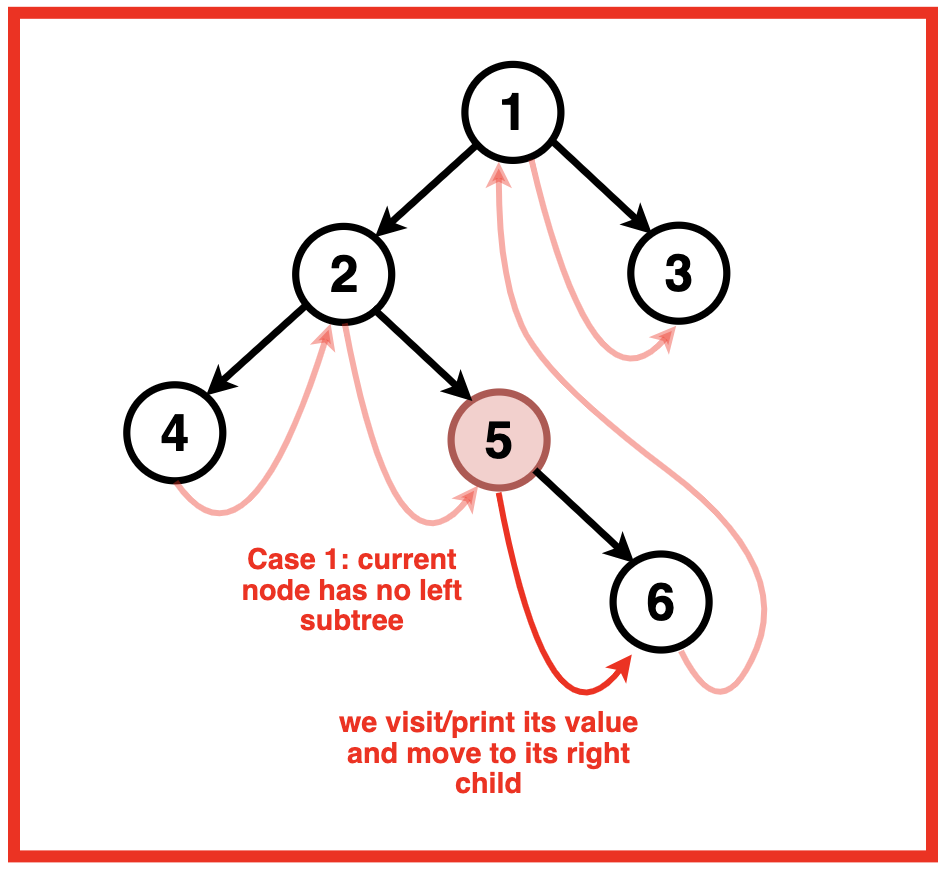
  如果没有左子树，我们只需打印当前节点的值，因为左侧没有节点可遍历。之后，我们移至右子节点继续遍历。

情况 2：存在一棵左子树，并且该左子树的最右边的孩子指向空。

• 将左子树的最右边的子节点设置为指向当前节点。
• 移动到当前节点的左子节点。
  
  
  
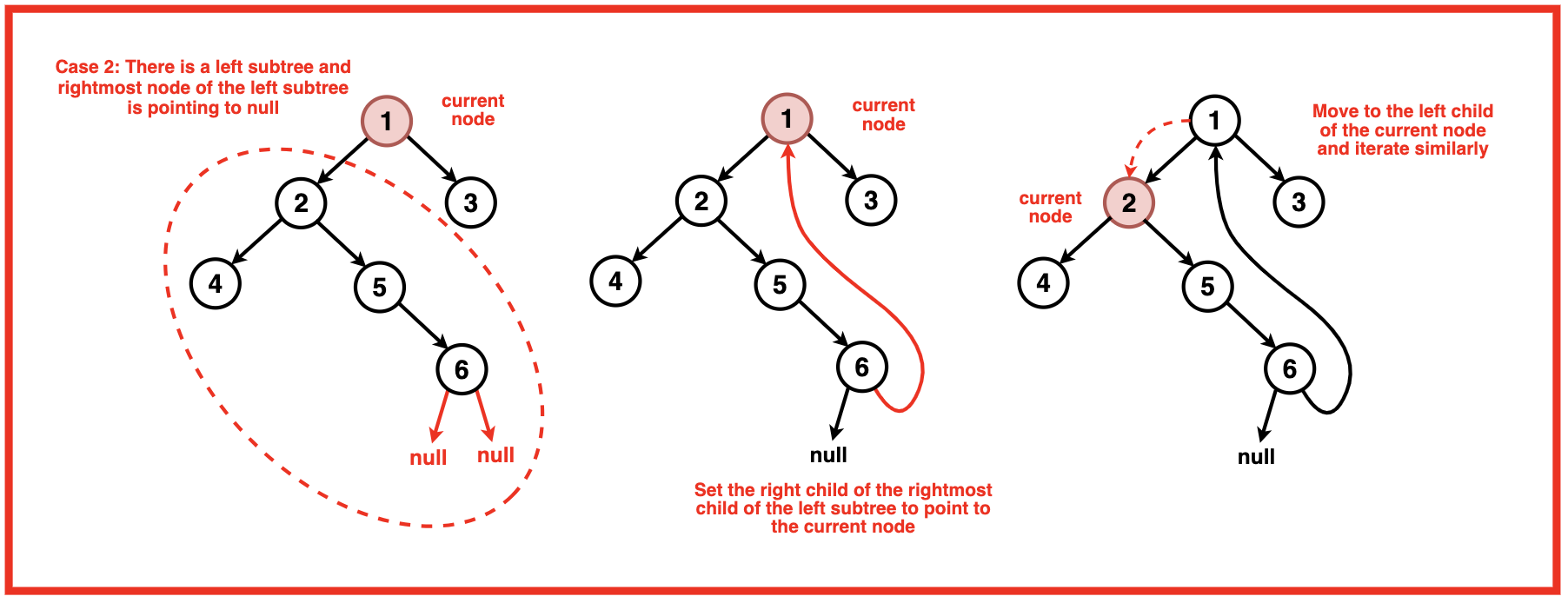
  在这种情况下，我们还没有访问左子树。我们从左子树的最右节点到当前节点建立一个临时链接。此链接可帮助我们稍后确定何时完成左子树的按序遍历。设置链接后，我们移至左子节点以探索左子树。

情况3：存在一棵左子树，并且该左子树的最右边的孩子已经指向当前节点。

• 打印当前节点的值
• 恢复临时链接（将其设置回空）
• 移动到当前节点的右子节点。
  
  
  
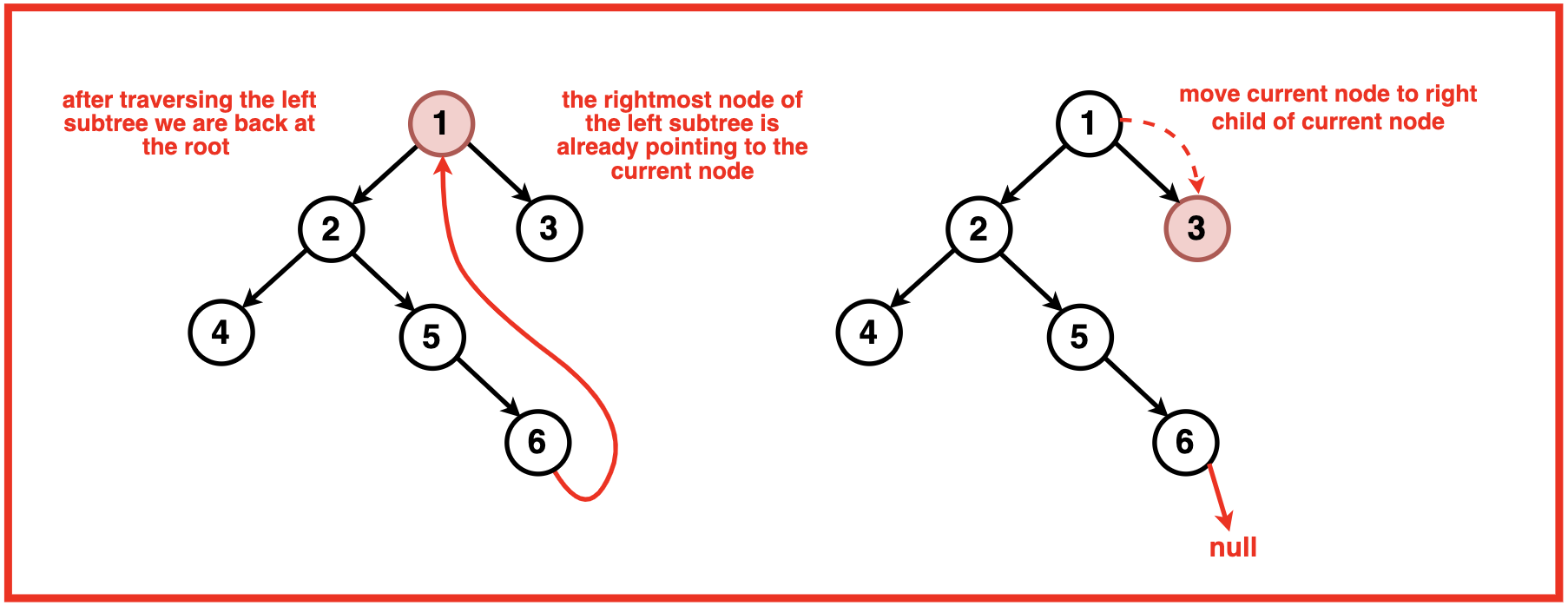
  这种情况对于保持树结构的完整性至关重要。如果左子树的最右边的子节点已经指向当前节点，则意味着我们已经完成了左子树的按序遍历。我们打印当前节点的值，然后恢复临时链接以恢复原始树结构。最后，我们移动到右子节点继续遍历。

算法

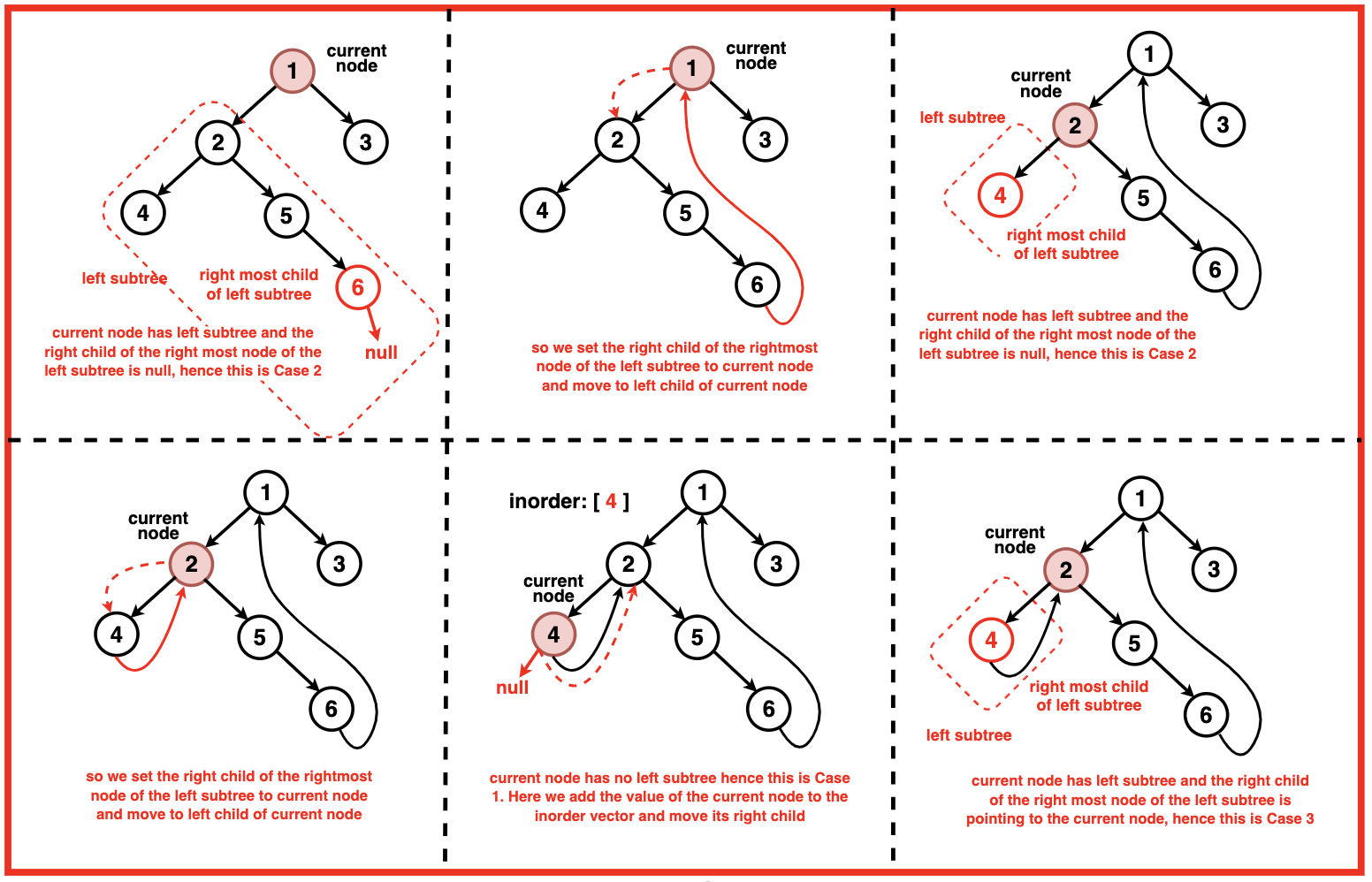
步骤 1：初始化 current 来遍历树。将 current 设置为二叉树的根。

步骤 2：当前节点不为空时：如果当前节点没有左子节点，则打印当前节点的值并移动到右子节点，即将当前节点设置为其右子节点。

步骤 3： 当前节点有左孩子，我们找到当前节点的 in-order predecessor 。这个 in-order predecessor 是左子树的最右节点。

• 如果 in-order predecessor 的右孩子节点为空：
  • 将 in-order predecessor 右孩子节点设置为当前节点。
  • 移动到 current 的左孩子
• 如果 in-order predecessor 的右孩子不为空：
  • 通过in-order predecessor 的右孩子设置为空
  • 打印当前节点的值。
  • 通过先前 in-order predecessor 的右孩子拿到 current , 然后移动到 cuurent 的右孩子节点
    
    重复步骤 2 和 3，直到到达树的末尾。

代码实现

#include <iostream>
#include <sstream>
#include <unordered_map>
#include <vector>
#include <queue>
#include <map>

using namespace std;

// TreeNode structure
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

class Solution {
public:
    // Function to perform iterative Morris
    // inorder traversal of a binary tree
    vector<int> getInorder(TreeNode* root) {
        // Vector to store the
        // inorder traversal result
        vector<int> inorder;
        // Pointer to the current node,
        // starting from the root
        TreeNode* cur = root;

        // Loop until the current
        // node is not NULL
        while (cur != NULL) {
            // If the current node's
            // left child is NULL
            if (cur->left == NULL) {
                // Add the value of the current
                // node to the inorder vector
                inorder.push_back(cur->val);
                // Move to the right child
                cur = cur->right;
            } else {
                // If the left child is not NULL,
                // find the predecessor (rightmost node
                // in the left subtree)
                TreeNode* prev = cur->left;
                while (prev->right && prev->right != cur) {
                    prev = prev->right;
                }

                // If the predecessor's right child
                // is NULL, establish a temporary link
                // and move to the left child
                if (prev->right == NULL) {
                    prev->right = cur;
                    cur = cur->left;
                } else {
                    // If the predecessor's right child
                    // is already linked, remove the link,
                    // add current node to inorder vector,
                    // and move to the right child
                    prev->right = NULL;
                    inorder.push_back(cur->val);
                    cur = cur->right;
                }
            }
        }

        // Return the inorder
        // traversal result
        return inorder;
    }
};

int main() {

    TreeNode* root = new TreeNode(1);
    root->left = new TreeNode(2);
    root->right = new TreeNode(3);
    root->left->left = new TreeNode(4);
    root->left->right = new TreeNode(5);
    root->left->right->right = new TreeNode(6);

    Solution sol;

    vector<int> inorder = sol.getInorder(root);

    cout << "Binary Tree Morris Inorder Traversal: ";
    for(int i = 0; i< inorder.size(); i++){
        cout << inorder[i] << " ";
    }
    cout << endl;

    return 0;
}