揭秘GES超大规模图计算引擎HyG：图切分

摘要：GES大规模图计算引擎HyG通过实现不同的点边分区算法，可以灵活地供用户选择多种多样的切分策略，进而达到更好的运算性能。

本文分享自华为云社区《GES超大规模图计算引擎HyG揭秘之图切分》，作者：π 。

对于超大规模图数据，点、边数量可以达到百亿甚至千亿、万亿，存储如此规模的图数据往往需要几百GB甚至几TB的存储空间，为了高效的图计算分析，往往需要将图数据存储于内存中，因此，对于超大规模的图数据，是没有办法将整张图存放在单机之上的，这就需要图计算框架对原始图进行切分，将一张大图切割成多个子图，然后将这些子图运行于一个集群之上，进而完成各种各样的图分析、图查询任务。GES大规模图计算引擎HyG通过实现不同的点边分区算法，可以灵活地供用户选择多种多样的切分策略，进而达到更好的运算性能。

一个好的图切分算法对于图计算引擎性能至关重要：

合理的切分可以使每个子图负载更加均衡，进而加快每轮的迭代速度
合理的切分可以大大降低子图之间的通信开销

图切分算法主要有两大分支：

离线切分：需要加载完整的图数据，根据图整体的拓扑结构，进行多次迭代、聚类等方法，来获得高质量的分区边界
流式切分：在对点/边的划分过程中，被划分对象数据流式地传输到图划分模块中，当前对象的分区策略至多依赖于之前对象的分区状态，而与后续流式传输来的对象的信息无关

流式的图分区算法的优点

1) 内存占用小。流式的图分区算法每个分区只需要加载部分的图数据即可进行划分，各分区之间只需要较小的通讯代价即可完成对分区状态的同步。而离线的图分区算法需要加载完整的图数据，并且例如XtraPupl、Metis对整个图进行多次迭代，细化其分区，产生大量内存开销。

2) 分图效率高。流式的图分区算法中，对象流式地传入，即刻可以决定分区结果，对每个分区对象只需要遍历一次。并且支持多线程多个对象并行流式输入、分区，分区完成之后线程间同步分区状态，实现高效率的分区。而类似XtraPupl、Metis的离线分区算法，由于需要多次迭代，对一个对象的分区需要对遍历不止一次，并且由于其分区算法对图整体拓扑结构的依赖性高，导致其可开发的并行度不高，分图效率不如流式的图分区算法。

3) 分图质量相当，部分情况下更优。在对多种图计算算法和多个数据集的测试中，图计算推理时间开销各有优劣，但流式图分区中总有数个具体分区算法，其在图计算推理的时间开销优于离线图分区算法XtraPupl，用户使用流式图分区算法具有更高的灵活度，可以针对不同的算法、数据集、分区数量，选择合适的具体分区算法，获得更好的图计算推理性能。

我们的HyG图计算引擎就是采用流式切分算法进行图切分。

HyG图计算引擎如何实现图切分？

图切分最核心的就是两个步骤。1、如何将点分配到各个主机；2、如何将边分配到各个主机。HyG对这两个步骤进行了抽象，定义了以下两个方法：

getMaster(nodeID) //给定一个点ID，返回这个点需要分配给哪个主机

getEdgeOwner(edgeSrcID, edgeDstID) // 给定一条边，返回这个边需要分配给哪个主机

一旦给出了以上两个函数，HyG的切分器就可以完成大图的切分。业界和学术界有大量的图切分算法，本质的区别就是getMaster和getEdgeOwner的实现不同，几乎所有的图切分算法都可以重写成这种模式。下面我们举一个出边切（OEC）的例子，看看HyG是怎么通过重定义getMaster和getEdgeOwner两个函数完成图切分的。

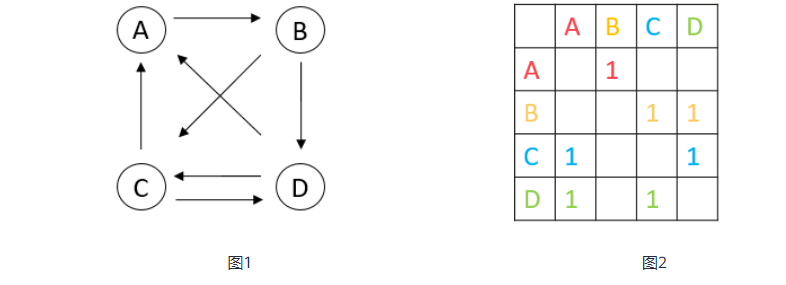
首先我们定义

GetMaster(nodeID)

    return ﬂoor(nodeID / hostNum)

这个函数很简单，就是点ID除以主机数量然后向下取整，图1我们有4个顶点，假设我们有4个主机，这样的话就为每个主机分配了一个点。

然后我们定义

GetEdgeOwner(edgeSrcID, edgeDstID)

    return masterOf(edgeSrcID)

这个函数也很简单，就是获取边的源顶点所在的主机ID，因为GetMaster已经完成了点的划分，因此这一步直接查询就可以得到结果。这样的话切分器就明确了这条边应该分配给哪个主机。

在完成GetMaster和GetEdgeOwner的定义后，HyG就可以将原始的图切分成4个子图，如图3所示。

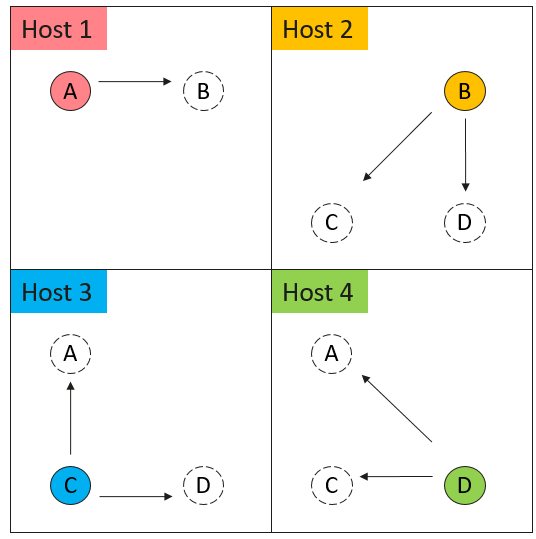
图3

上面提到的切分示例是最简单的一种切分方法，在现实应用场景下，往往需要更为复杂的切分策略才能达到有效、均衡的切分效果。

HyG实现的点分区算法主要分为两类：ContiguousEB和FennelEB。

1) ContiguousEB直接将点分配给在读图阶段读取该点的分区，不进行额外的分区操作。

2) FennelEB在分区时会维护当前的分区状态，流式读取到顶点后，会根据各分区的已分配数量、该顶点在各分区的局部性，为每个分区生成一个评分，将顶点分配到评分最高的分区中。

HyG实现的边分区算法主要分为三类：Source，Hybrid和Cartesian。

1) Source直接将边分配给其对应顶点所在的分区，如果是以出边划分的算法，即将其划分给源顶点所在的分区，如果是以入边划分的算法，即将其划分给目标顶点所在的分区。

2) Hybrid设定一个阈值threshold，顶点度数低于阈值的称为低度顶点，高于阈值的视为高度顶点。这种边分区算法保证了低度顶点的局部性，同时将高度顶点分散开来，避免了少数高度顶点带来的负载不均衡问题。

3) Cartesian将邻接矩阵切分为数个二维网格，每个网格对应一个分区，将边按照网格划分，这种分区算法保留了一定的局部性，同时可以获得更好的负载均衡。

HyG通过实现不同的点分区算法（GetMaster）和不同的边分区算法（GetEdgeOwner），可以实现多种多样的切分策略，非常的灵活好用，用户可以根据自己图数据的特点选择不同的切分策略，进而达到更好的运算性能。

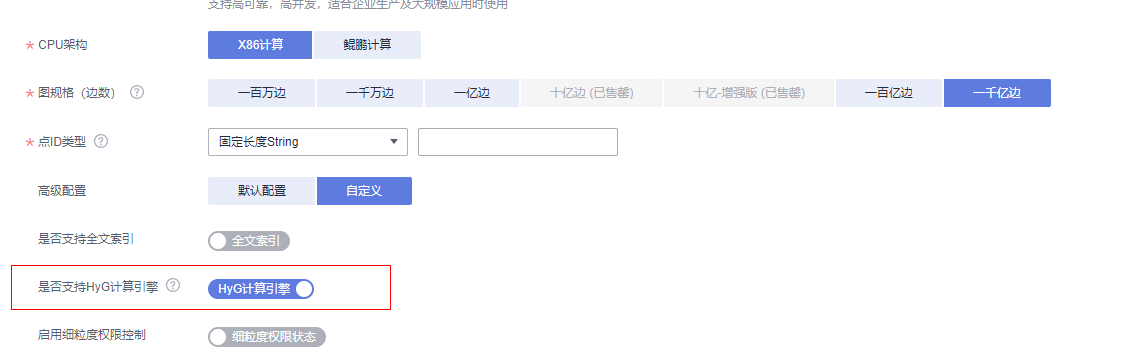
目前HyG已上线至华为云GES服务，欢迎大家上手体验~

点击关注，第一时间了解华为云新鲜技术~