cf938D

题意简述：n个点m条边的无向图，有点权，有边权， 对于每一个点计算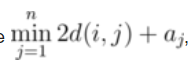，d(i,j)表示点i到点j的最短路

题解：边权扩大二倍，建立源点，然后源点向每一个点x连接一条权值为a[x]的边，然后跑最短路即可

#include<bits/stdc++.h>

#define forn(i, n) for (int i = 0; i < int(n); i++)
#define fore(i, s, t) for (int i = s; i < (int)t; i++)
#define fi first
#define se second
#define all(x) x.begin(),x.end()
#define pf2(x,y) printf("%d %d\n",x,y)
#define pf(x) printf("%d\n",x)
#define each(x) for(auto it:x)  cout<<it<<endl;
#define pi pair<int,int>

using namespace std;

char inline nc(){
    static char buf[100000],*p1=buf,*p2=buf;
    return p1==p2&&(p2=(p1=buf)+fread(buf,1,100000,stdin),p1==p2)?EOF:*p1++;
}

template <typename T>
bool rd(T& v){
    static char ch;
    while(ch!=EOF&&!isdigit(ch)) ch=nc();
    if(ch==EOF) return false;
    for(v=0;isdigit(ch);ch=nc())
        v=v*10+ch-'0';
    return true;
}

template <typename T>
void o(T p){
    static int stk[70],tp;
    if(p==0) {
        putchar('0');return ;
    }
    if(p<0) {
        p=-p;putchar('-');
    }
    while(p) stk[++tp]=p%10,p/=10;
    while(tp) putchar(stk[tp--]+'0');
}

typedef long long ll;

const int maxn=2e5+5;
const int maxm=6e5+5;
const int inf=1e9;

int head[maxn],ver[maxm],nex[maxm],tot;

ll wi[maxm];

int n,m;

void inline AddEdge(int x,int y,ll z){
	ver[++tot]=y,wi[tot]=z,nex[tot]=head[x],head[x]=tot;
}

ll dis[maxn];

bool vis[maxn];

void dijkstra(){
	memset(dis,0x3f,sizeof(dis));
	dis[n+1]=0;
	multiset<pair<ll,int>> q;
	q.insert({0,n+1});
	while(q.size()){
		int x=q.begin()->se;q.erase(q.begin());
		if(vis[x]) continue;
		vis[x]=1;
		for(int i=head[x];i;i=nex[i]){
			int y=ver[i];
			if(dis[y]>dis[x]+wi[i]){
				dis[y]=dis[x]+wi[i];
				q.insert({dis[y],y});
			}
		}
	}
}
int main(){
	ios_base::sync_with_stdio(false);
	cin>>n>>m;
	for(int i=0;i<m;i++){
		int x,y;ll z;
		cin>>x>>y>>z;
		AddEdge(x,y,2*z);
		AddEdge(y,x,2*z);
	}
	for(int i=0;i<n;i++){
		ll x;
		cin>>x;
		AddEdge(n+1,i+1,x);
	}
	dijkstra();
	for(int i=1;i<=n;i++)
		cout<<dis[i]<<' ';
	cout<<"\n";
}