C语言用两个栈实现队列(完整版)

队列是一种 先进先出（first in - first out， FIFO）的数据结构，队列中的元素都从后端（rear）入队（push），从前端（front）出队（pop）。
实现队列最直观的方法是用链表，但在这篇文章里我会介绍另一个方法 - 使用栈。
栈是一种 后进先出（last in - first out， LIFO）的数据结构，栈中元素从栈顶（top）压入（push)，也从栈顶弹出（pop）。
为了满足队列的 FIFO 的特性，我们需要用到两个栈，用它们其中一个来反转元素的入队顺序，用另一个来存储元素的最终顺序。

方法一（使用两个栈 入队 - O(n)O(n)， 出队 - O(1)O(1)）
算法

入队（push）思路：考虑入队的元素是先进先出，后进后出，而你的栈是后进先出，那么你最新压入的元素(后进的)应该在栈底，也就是只要保证后进后出即可

一个队列是 FIFO 的，但一个栈是 LIFO 的。这就意味着最新压入的元素必须得放在栈底。为了实现这个目的，我们首先需要把 s1 中所有的元素移到 s2 中，接着把新元素压入 s2。最后把 s2 中所有的元素弹出，再把弹出的元素压入 s1。

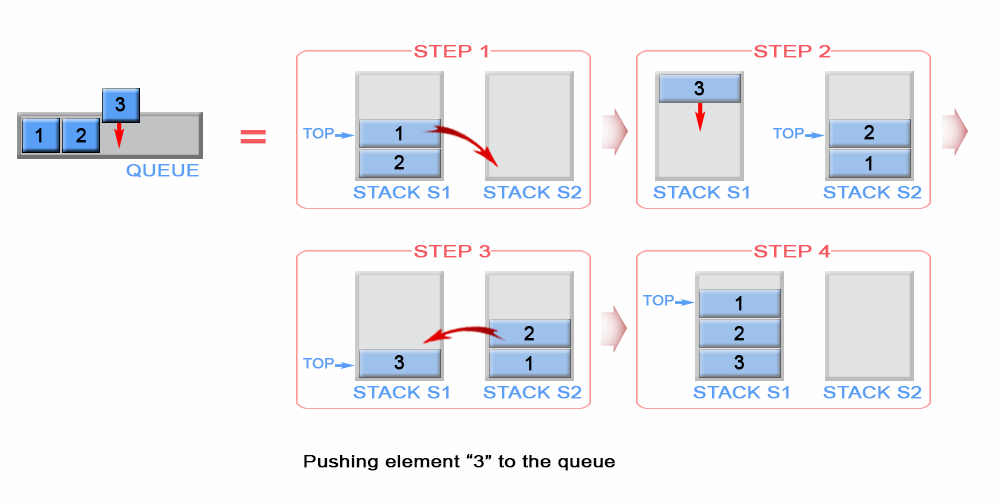
出队（pop）

直接从 s1 弹出就可以了，因为 s1 的栈顶元素就是队列的队首元素。同时我们把弹出之后 s1 的栈顶元素赋值给代表队首元素的 front 变量。

以上图片以及文字来自https://leetcode-cn.com/problems/implement-queue-using-stacks/solution/yong-zhan-shi-xian-dui-lie-by-leetcode/

#include <stdio.h>
#include <stdlib.h>
#define maxsize 100
//创建栈
struct Stack{
int data[maxsize];
int top;
};
typedef struct Stack MyStack;
//队列定义为双栈
typedef struct {
MyStack s1; //S1为主栈
MyStack s2; //S2为用来反转的栈
} MyQueue;

/** Initialize your data structure here. */

MyQueue* myQueueCreate() {
MyQueue * tempQueue =(MyQueue *)malloc(sizeof(MyQueue));
tempQueue->s1.top = -1 ;
tempQueue->s2.top = -1 ;
return tempQueue ;

}

/** Push element x to the back of queue. */
void myQueuePush(MyQueue* obj, int x) {
if(obj->s1.top<maxsize)
{
while(obj->s1.top!=-1) //栈是否满
{
obj->s2.data[++(obj->s2.top)]=obj->s1.data[(obj->s1.top)--];////把S1栈中元素压入S2实现反转
}
obj->s1.data[++(obj->s1.top)]= x ; ////把push的元素压入S1栈（此时S1为空栈，因为它的元素已经全部给S2啦）
while(obj->s2.top!=-1)
{
obj->s1.data[++(obj->s1.top)]=obj->s2.data[(obj->s2.top)--];//再把S2栈中的元素全部反转压入S1
}
}
}
void show_myQueue(MyQueue * obj)
{
int temp =obj->s1.top ;
while(temp!=-1)
{
printf("%d ",obj->s1.data[temp--]);
}
printf("\n");
}

/** Removes the element from in front of queue and returns that element. */
int myQueuePop(MyQueue* obj) {
if(obj->s1.top!=-1)
{
return obj->s1.data[obj->s1.top--] ;
}
// return NULL ;

}

/** Get the front element. */
int myQueuePeek(MyQueue* obj) {
if(obj->s1.top!=-1)
{
return obj->s1.data[obj->s1.top] ;
}
// return NULL ;
}

/** Returns whether the queue is empty. */
bool myQueueEmpty(MyQueue* obj) {
if(obj->s1.top == -1)
return true ;
return false ;

}

void myQueueFree(MyQueue* obj) {
free(obj);
}

int main()
{
int i ;
MyQueue * myQueue =NULL;
myQueue =myQueueCreate();
for(i=0;i<3;i++)
{
myQueuePush(myQueue,i);
}
show_myQueue(myQueue);
printf("出队的元素是:%d\n",myQueuePop(myQueue));
printf("此时队列内的首个的元素是:%d\n",myQueuePeek(myQueue));
}

/**
* Your MyQueue struct will be instantiated and called as such:
* MyQueue* obj = myQueueCreate();
* myQueuePush(obj, x);

* int param_2 = myQueuePop(obj);

* int param_3 = myQueuePeek(obj);

* bool param_4 = myQueueEmpty(obj);

* myQueueFree(obj);
*/