LeetCode 858 镜面反射

题目

有一个特殊的正方形房间，每面墙上都有一面镜子。除西南角以外，每个角落都放有一个接受器，编号为 0， 1，以及 2。

正方形房间的墙壁长度为 p，一束激光从西南角射出，首先会与东墙相遇，入射点到接收器 0 的距离为 q 。

返回光线最先遇到的接收器的编号（保证光线最终会遇到一个接收器）。

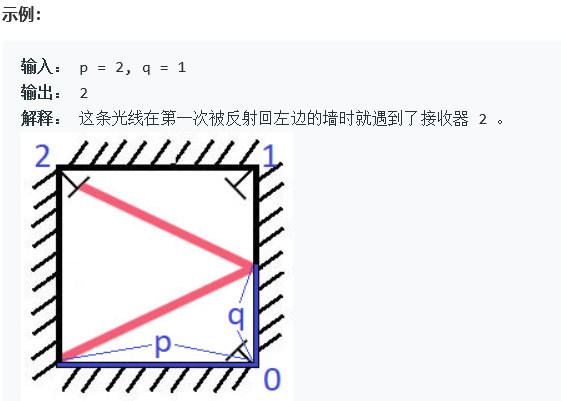
思路

本题若单纯依靠镜面反射的思想非常复杂难以解决问题，必须将问题转化。

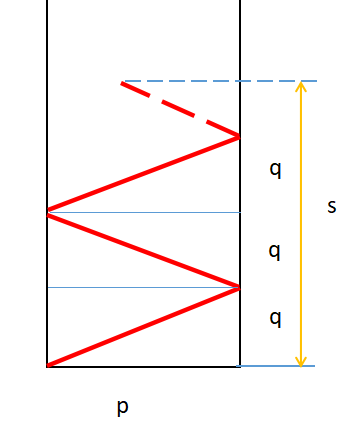
1.我们假设东西两面墙无限向北拉长，将北墙暂时忽略，使得光线只有向上的反射。

2.当向上的纵距离第一次为p的整数倍时，可认为光线到达其中一个接收器。

3.通过观察画图可以发现，这个纵向距离是p和q的最小公倍数，设为s。

4.如何去判断光线遇到哪个接收器？分两步

a.首先确定是光线到达南墙还是北墙(判断s/p奇偶)；

b.若是南墙(s/p为偶)直接返回接收器0；若是北墙(s/p为奇)还需确定是接受器1还是2(判断s/q奇偶)；

代码

class Solution {
public:
    int mirrorReflection(int p, int q) {
        int s=lcm(p,q);//最小公倍数等于纵向距离
        if((s/p)%2==0){//若南北次数为偶，则为南墙，0
            return 0;
        }
        else{//为奇北墙
            if((s/q%2)==1)return 1;//若东西次数为奇，则东墙，1
            else return 2;//为偶西墙，2
        }
    }
    int gcd(int a, int b){//最大公约数
        return a % b ? gcd(b, a % b) : b;
    }
    int lcm(int a, int b){//最小公倍数
        return a * b / gcd(a, b);
    }
};