[剑指offer]10.斐波那契数列+青蛙跳台阶问题

10- I. 斐波那契数列

方法一 Top-down

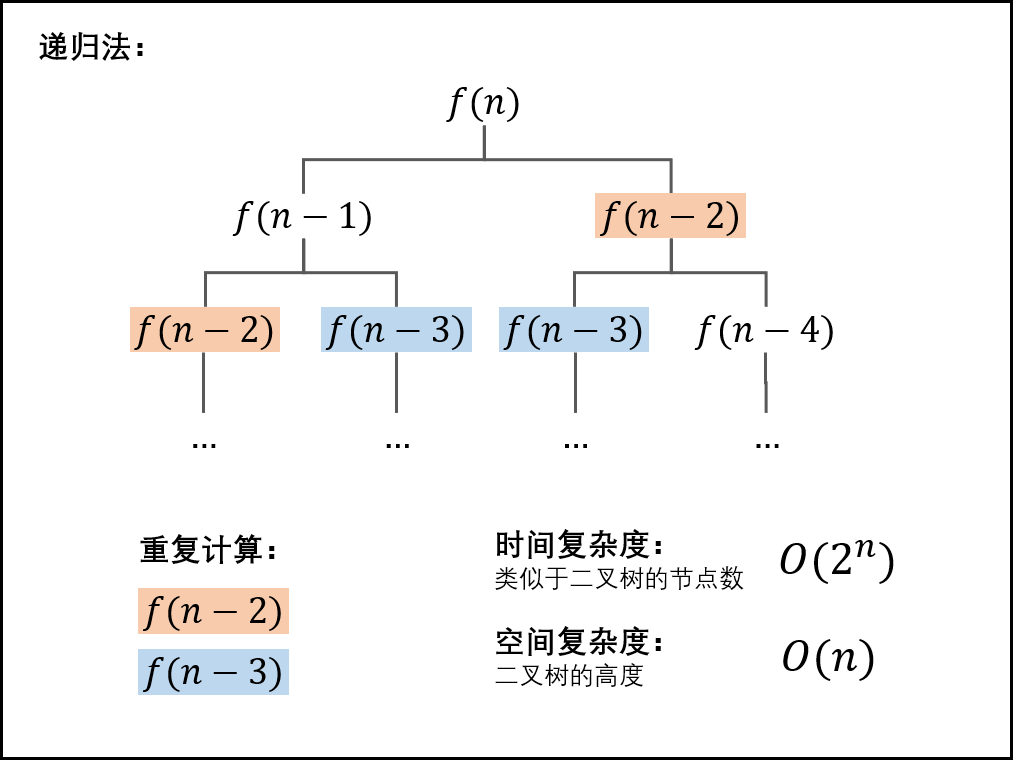
用递归实现

def fibonacci(n):
    if n <= 0:
        return 0
    if n == 1:
        return 1
    return fibonacci(n-1) + fibonacci(n-2)

不过这种方法在leetcode上超时了。

方法二 Bottom-up

用循环实现

class Solution:
    def fib(self, n: int) -> int:
        if n <= 0:
            return 0
        if n == 1:
            return 1
        tmp = 0
        fibNMinusOne = 1
        fibNMinusTwo = 0
        for i in range(2, n+1):
            tmp = fibNMinusOne + fibNMinusTwo
            fibNMinusTwo = fibNMinusOne
            fibNMinusOne = tmp
        return tmp

面试题10- II. 青蛙跳台阶问题

思路：把它转化为一个Fibonacci问题。

设青蛙跳n级台阶，共numWays(n)种方法；

如果青蛙第一次跳一级台阶，则剩下的n-1级台阶共numWays(n-1)种跳法；

如果青蛙第一次跳两级台阶，剩下的n-2级台阶共numWays(n-2)种跳法；

故numWays(n) = numWays(n-2) + numWays(n-1)，即为递推公式。

代码

class Solution:
    def numWays(self, n: int) -> int:
        res = [1, 1, 2]
        if n <= 2:
            return res[n]
        fibN = 0
        fibNMinusTwo = 1
        fibNMinusOne = 2
        for i in range(3, n+1):
            fibN = fibNMinusOne + fibNMinusTwo
            fibNMinusTwo = fibNMinusOne
            fibNMinusOne = fibN
        return fibN%1000000007