网络流的最大流入门（从普通算法到dinic优化）

网络流(network-flows)是一种类比水流的解决问题方法，与线性规划密切相关。网络流的理论和应用在不断发展。而我们今天要讲的就是网络流里的一种常见问题——最大流问题。

最大流问题(maximum flow problem)，一种组合最优化问题，就是要讨论如何充分利用装置的能力，使得运输的流量最大，以取得最好的效果。求最大流的标号算法最早由福特和福克逊与与1956年提出，20世纪50年代福特(Ford)、(Fulkerson)建立的“网络流理论”，是网络应用的重要组成成分。

再解决这个问题前，我们要先弄懂一些定义：

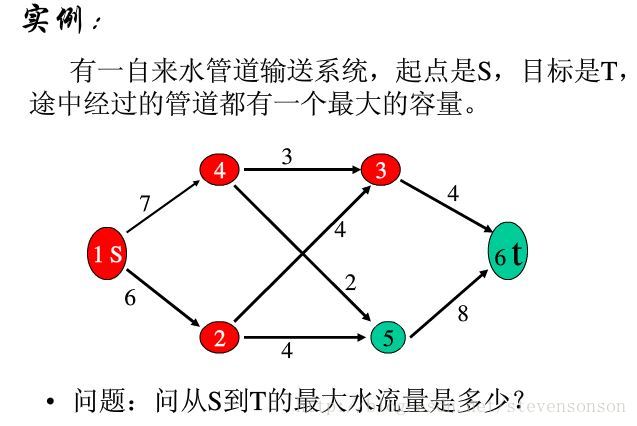
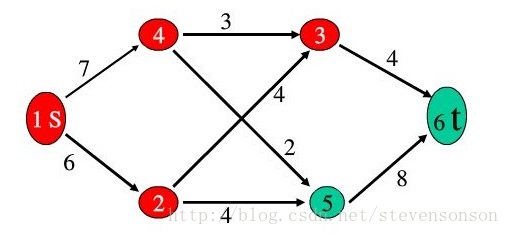
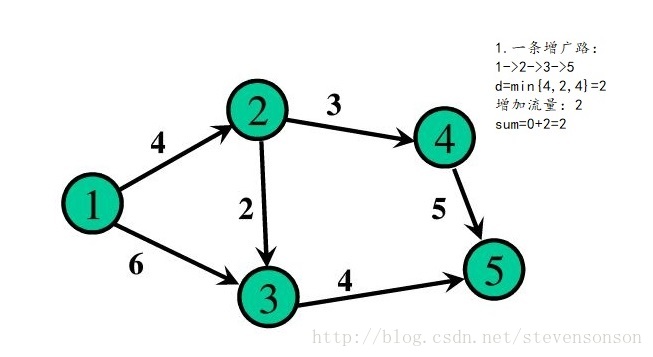
网络流图是一张只有一个源点和汇点的有向图，而最大流就是求源点到汇点间的最大水流量，下图的问题就是一个最基本，经典的最大流问题

二.流量，容量和可行流

对于弧(u,v)来说，流量就是其上流过的水量(我们通常用f(u,v)表示)，而容量就是其上可流过的最大水量(我们通常用c(u,v)表示)，只要满足f(u,v)<=c(u,v)，我们就称流量f(u,v)是可行流(对于最大流问题而言，所有管道上的流量必须都是可行流)。

三.增广路

如果一条路上的所有边均满足:

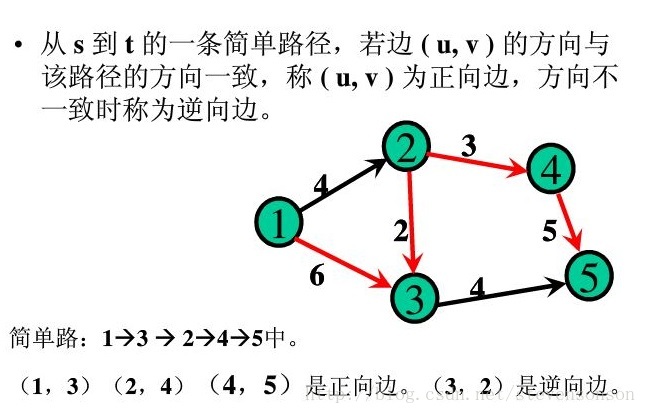
正向边: f(u,v)< c(u,v) ——– 反向边：f(u,v)> 0

假如有这么一条路，这条路从源点开始一直一段一段的连到了汇点，并且，这条路上的每一段都满足流量<容量，注意，是严格的<,而不是<=。那么，我们一定能找到这条路上的每一段的(容量-流量)的值当中的最小值delta。我们把这条路上每一段的流量都加上这个delta，一定可以保证这个流依然是可行流。这样我们就得到了一个更大的流，他的流量是之前的流量+delta，而这条路就叫做增广路. From 网络流(Network Flow)

则我们称这条路径为一条增广路径，简称增广路。

好了，弄懂了一些定义，接下来就可以介绍著名的Ford-Fulkerson算法了。

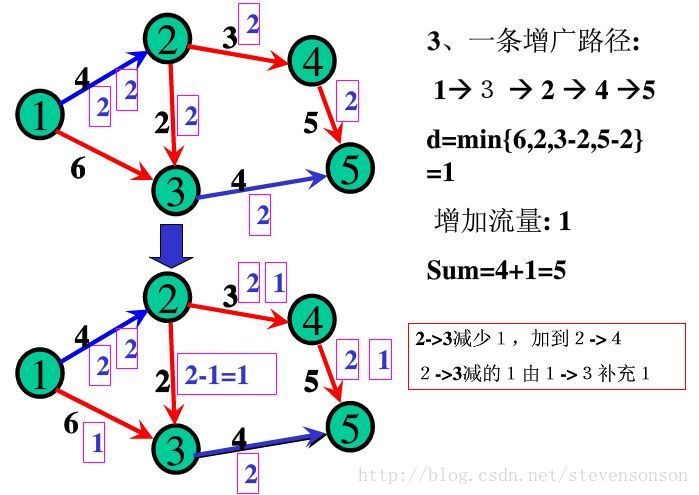
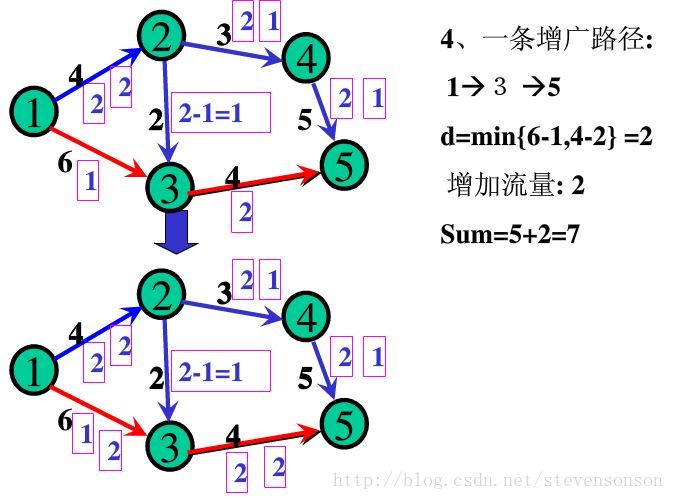
如图所示，如果我们每次都找出一条增广路，只要这条增广路经过汇点，那说明此时水流还可以增加，增加的量为d(d=min(d,c(u,v)-f(u,v))或d=min(d,f(u,v)))。

我们可以这样理解：对于每一条正向边，他能添加的最大水流为c(u,v)-f(u,v)。而对于反向边来说，当正向边上的水流增多时，反向边自身的反向水流会减少，而其能减少的最多水量为f(u,v)。由于要保证添加水流之后，所有的f(u,v)都是可行流，所以我们取最小值。

增加之后，我们要更新流量，每条正向边+d,每条反向边-d即可。

既然这样，我们的思路就是：

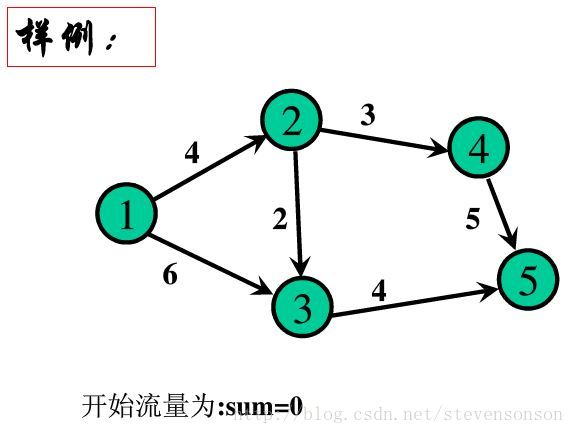
1.找出一条增广路径 ——2.修改其上点的值——3.继续重复1，直至找不出增广路。则此时源点的汇出量即为所求的最大流。

那么上代码：

#include<bits/stdc++.h>
#include<vector>
#define maxn 1200
#define INF 2e9
using namespace std;
int i,j,k,n,m,h,t,tot,ans,st,en;
struct node{
    int c,f;
}edge[maxn][maxn];
int flag[maxn],pre[maxn],alpha[maxn],q[maxn],v;
int read(){
    char c;int x;while(c=getchar(),c<'0'||c>'9');x=c-'0';
    while(c=getchar(),c>='0'&&c<='9') x=x*10+c-'0';return x;
}

void bfs(){
    memset(flag,0xff,sizeof(flag));memset(pre,0xff,sizeof(pre));memset(alpha,0xff,sizeof(alpha));
    flag[st]=0;pre[st]=0;alpha[st]=INF;h=0,t=1;q[t]=st;
    while(h<t){
        h++;v=q[h];
        for(int i=1;i<=n;i++){
            if(flag[i]==-1){
                if(edge[v][i].c<INF&&edge[v][i].f<edge[v][i].c){
                    flag[i]=0;pre[i]=v;alpha[i]=min(alpha[v],edge[v][i].c-edge[v][i].f);q[++t]=i;
                }
                else if(edge[i][v].c<INF&&edge[i][v].f>0){
                    flag[i]=0;pre[i]=-v;alpha[i]=min(alpha[v],edge[i][v].f);q[++t]=i;
                }
            }
        }
        flag[v]=1;
    }
}

void Ford_Fulkerson(){
    while(1){
        bfs();
        if(alpha[en]==0||flag[en]==-1){
            break;
        }
        int k1=en,k2=abs(pre[k1]);int a=alpha[en];
        while(1){
            if(edge[k2][k1].c<INF) edge[k2][k1].f+=a;
            else if(edge[k1][k2].c<INF) edge[k1][k2].f-=a;
            if(k2==st) break;
            k1=k2;k2=abs(pre[k1]);
        }
        alpha[en]=0;
    }
}

void flow(){
    int maxflow=0;
    for(int i=1;i<=n;i++)
      for(int j=1;j<=n;j++){
        if(i==st&&edge[i][j].f<INF) maxflow+=edge[i][j].f;
      }
    printf("%d",maxflow);
}

int main(){
    int u,v,c,f;
    n=read();m=read();st=read();en=read();
    for(int i=1;i<=n;i++)
      for(int j=1;j<=n;j++) edge[i][j].c=INF,edge[i][j].f=0;
    for(int i=1;i<=m;i++){
        u=read();v=read();c=read();
        edge[u][v].c=c;
    }
    Ford_Fulkerson();
    flow();
    return 0;
}