2019-2020-1 20199324《Linux内核原理与分析》第三周作业

第二章 操作系统是如何工作的

一.知识点总结

1.计算机的三个法宝

• 存储程序计算机
• 函数调用堆栈机制。堆栈：是C语言程序运行时必须使用的记录函数调用路径和参数存储的空间。
• 中断

2.堆栈相关的寄存器和堆栈操作

• ESP（栈顶指针寄存器）：堆栈指针（指向栈顶）
• EBP（基址指针寄存器）：基址指针（指向栈顶），在C语言中用作记录当前函数调用的基址。
• EAX：用于暂存一些数值，函数返回值默认使用EAX寄存器存储并返回给上一级调用函数。
• EIP：指示将要执行的下一条指令在存储器中的地址。（总是指向某一条指令的地址）
• CS（代码段寄存器）
• push 压栈，栈顶地址减少四个字节
• pop 出栈，栈顶地址增加四个字节
• call 函数调用，调用一个地址。将当前CS:EIP的值压入栈顶，CS:EIP指向被调用函数的入口地址。
• ret 函数返回，从栈顶弹出原来保存在这里的CS:EIP的值，放入CS:EIP中去。
• enter 用来建立函数堆栈
• leave 用来撤销函数堆栈

3.内嵌汇编

/*
**通过例子来熟悉内嵌汇编的语法规则
*/

#include <stdio.h>

int main(){

    unsigned int val1 = 1;
    unsigned int val2 = 2;
    unsigned int val3 = 0;
    printf("val1:%d,val2:%d,val3:%d\n",val1,val2,val3);

    asm volatile(
    "movl $0,%%eax\n\t"        //把EAX清0
    "addl %1,%%eax\n\t"        //把ECX的值与EAX寄存器求和，然后放到EAX寄存器中去。%eax += val1
    "addl %2,%%eax\n\t"        //把val2的值加上val2的值再放到EAX中。%eax += val2
    "movl %%eax,%0\n\t"        //val1+val2的值存储的地方放到内存val3中。val3 = %eax
    :  "=m" (val3)
    :  "c" (val1),"d" (val2)
    );

    printf("val1:%d+val2:%d=val3:%d\n",val1,val2,val3);

    return 0;
}

• 内嵌汇编常用的限定符

|||||||

|:--|:--|

|限定符|描述|

|"a"|将输入变量放入EAX|

|"b"|将输入变量放入EBX|

|"c"|将输入变量放入ECX|

|"d"|将输入变量放入EDX|

|"s"|将输入变量放入ESI|

|"D"|将输入变量放入EDI|

|"r"|将输入变量放入通用寄存器，也就是EAX,EBX,ECX,EDX,ESI,EDI中的一个|

|"eax"|破坏描述部分|

|"m"|内存变量|

|"="|操作数在指令中只是写的（输出操作数）|

|"+"|操作数在指令中是读写类型的（输入输出操作数）|

• 小结

  • 寄存器前面会多一个%转义字符，有两个%
  • 输出输入的编号分别为%1，%2，%3......
  • 嵌入式汇编的时候每一个输入或输出的部分前面都可以加一个限定符

4.虚拟一个x86的CPU硬件平台

重要指令

$ cd ~/LinuxKernel/linux-3.9.4
$ rm -rf mykernel
$ patch -p1 < ../mykernel_for_linux3.9.4sc.patch
$ make allnoconfig
$ make
$ qemu -kernel arch/x86/boot/bzImage /*查看搭建起来的内核启动效果*/

搭建起来的内核启动效果如下所示：

在Linux-3.9.4内核源代码根目录下进入mykernel目录，可以看到QEMU窗口输出的mymain.c和myinterrupt.c的代码。

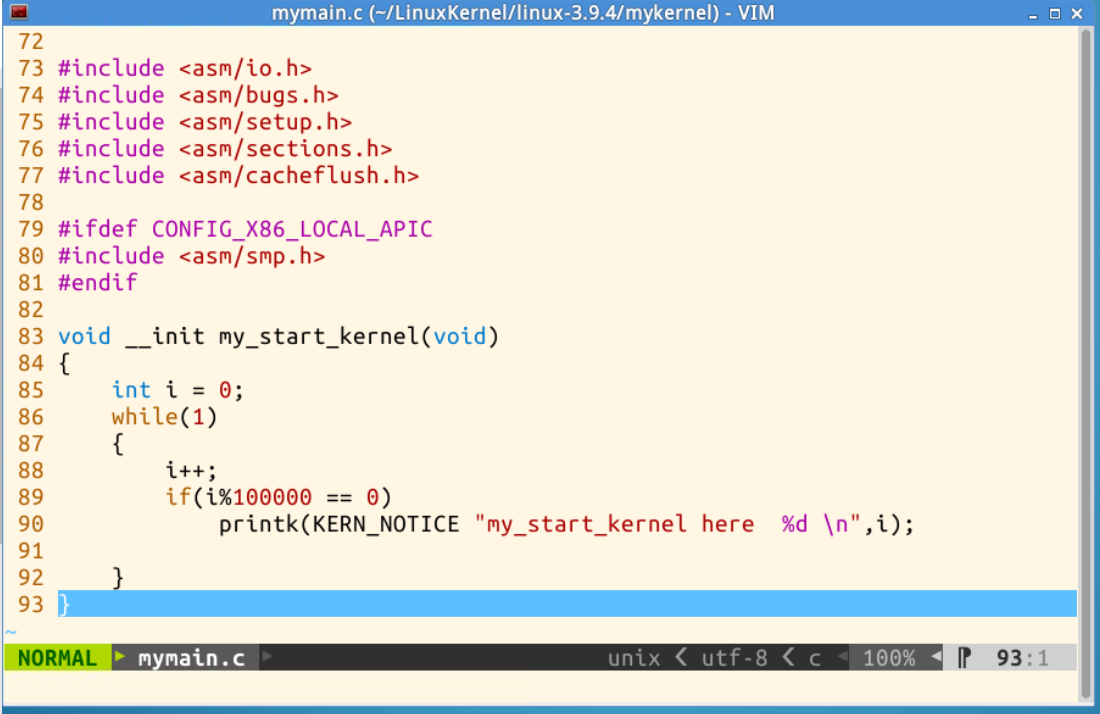
可以看到mymain.c中的函数my_start_kernel(void)函数，每执行100000次要输出“my_start_kernel here i”。



mymain.c中的代码在不停地被执行，同时有一个中断处理程序的上下文环境，周期性地产生时钟中断信号，能够触发mykernel.c中的my_timer_hander(void)函数。这样就模拟了一个带有时钟中断的x86CPU。

5.关键代码分析

• 1.mypcb.h头文件，用来定义进程控制块。

• 2.mymain.c 是mykernel内核代码的入口，负责初始化内核的各个组成部分。

asm volatile(
    	"movl %1,%%esp\n\t" 	/*将进程原堆栈的栈底的地址存入ESP寄存器中*/
    	"pushl %1\n\t" 	        /*将当前ESP寄存器的值入栈*/
    	"pushl %0\n\t" 	        /*将当前进程的EIP寄存器的值入栈*/
    	"ret\n\t" 	            /*让入栈的进程EIP保存到EIP寄存器中*/
    	"popl %%ebp\n\t"        /*这里不会被执行，只是一种编码习惯，与前面的push结对出现*/
    	:
    	: "c" (task[pid].thread.ip),"d" (task[pid].thread.sp)	/* input c or d mean %ecx/%edx*/
	);

堆栈变化：

• 3.myinterrupt.c 时钟中断处理和进程调度

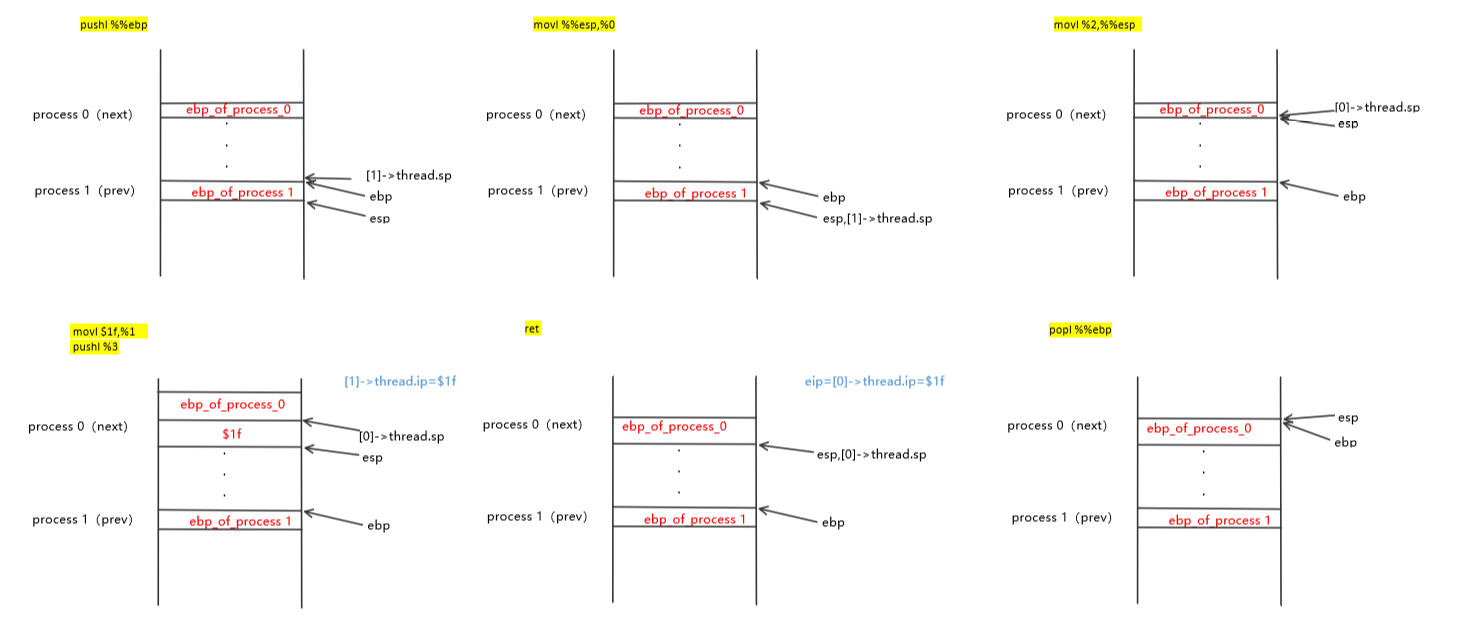
 if(next->state == 0)
    {
    	/*进程调度关键代码*/
    	asm volatile(
        	"pushl %%ebp\n\t" 	    /*保存当前EBP到堆栈*/
        	"movl %%esp,%0\n\t" 	/*保存当前ESP到当前PCB中*/
        	"movl %2,%%esp\n\t"     /*将next进程的堆栈栈顶的值存到ESP寄存器*/
        	"movl $1f,%1\n\t"       /*保存当前进程的EIP值，下次回复进程后将在标号1开始执行*/
        	"pushl %3\n\t"          /*将next进程继续执行的代码位置（标号1）压栈*/
        	"ret\n\t" 	            /*出栈标号1到eip寄存器*/
        	"1:\t"                  /*标号1，也就是next进程开始执行的位置*/
        	"popl %%ebp\n\t"        /*恢复EBP寄存器的值*/
        	: "=m" (prev->thread.sp),"=m" (prev->thread.ip)
        	: "m" (next->thread.sp),"m" (next->thread.ip)
    	); 

    	my_current_task = next;
    	printk(KERN_NOTICE ">>>switch %d to %d<<<\n",prev->pid,next->pid);
    } 

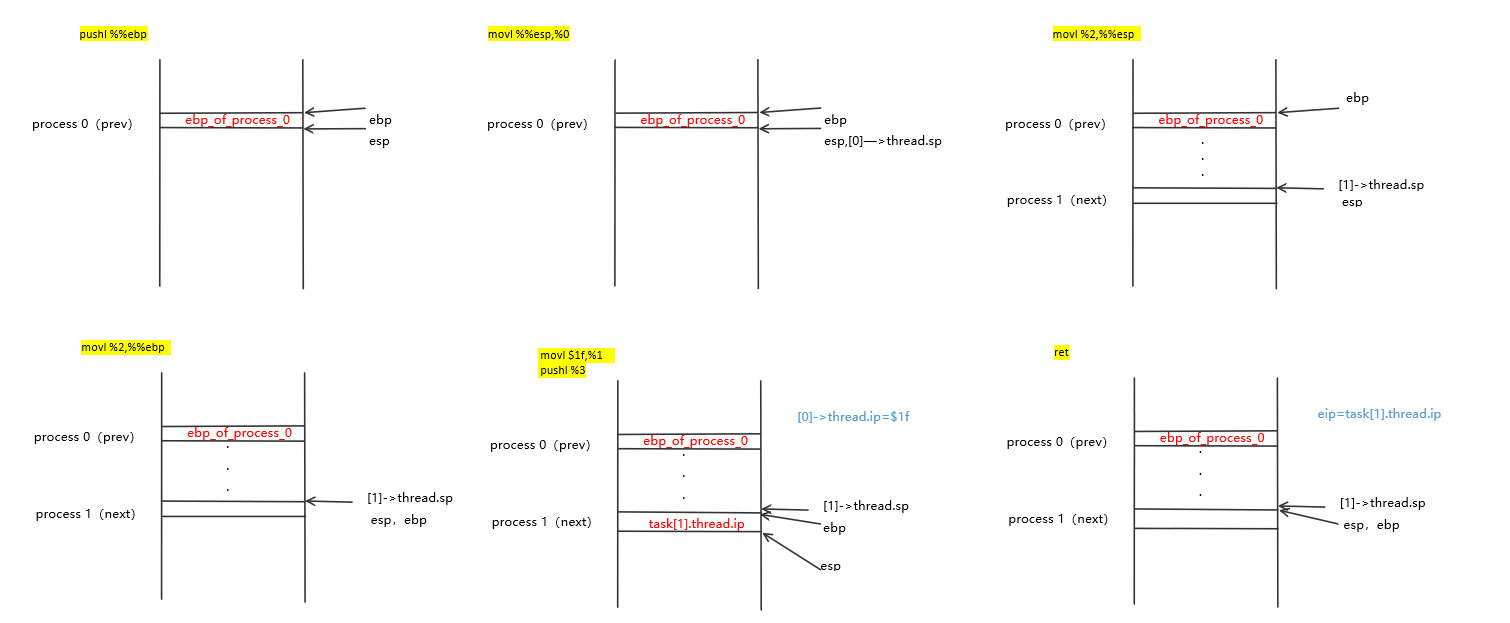
    else /*next该进程第一次被执行*/
    {
        next->state = 0;
        my_current_task = next;
        printk(KERN_NOTICE ">>>switch %d to %d<<<\n",prev->pid,next->pid);
        asm volatile(
        	"pushl %%ebp\n\t" 	    /*保存当前EBP到堆栈*/
        	"movl %%esp,%0\n\t" 	/*保存当前ESP到当前PCB中*/
        	"movl %2,%%esp\n\t"    	/*载入next进程的栈顶地址到ESP寄存器*/
        	"movl %2,%ebp\n\t"      /*载入next进程的堆栈基地址到EBP寄存器*/
        	"movl $1f,%1\n\t"       /*保存当前EIP寄存器值到PCB，这里$1f是指上面的标号1*/
        	"pushl %3\n\t"          /*把即将执行的进程的代码入口地址入栈*/
        	"ret\n\t" 	            /*出栈进程的代码入口地址到EIP寄存器*/
        	: "=m" (prev->thread.sp),"=m" (prev->thread.ip)
        	: "m" (next->thread.sp),"m" (next->thread.ip)
    	);
    }

假设系统只有两个进程分别为进程0和进程1。进程0由内核启动时初始化执行，进行进程调度，开始执行进程1。因为进程1从来没有被执行过，是第一次被执行，所以执行else中的代码。下面来分析进程1被调度的堆栈变化。

此时，开始执行进程1，如果进程1执行的过程中发生了进程调度，进程0重新被调度执行，此时应该执行if中的代码。if中的内嵌汇编代码执行过程中堆栈变化分析如下：