1D1D动态规划优化初步

再学习一下动态规划的基本优化方法…

首先这篇文章应该大家都看过吧…没看过的自行百度

关于实现的思路文章里都给好了…这篇就主要给一点题目啥的

（P.S. 电脑重装了，如果博客发出来有一些奇怪的问题不要在意）

模型一，即决策单调性优化

①玩具装箱 bzoj1010

题目自己看去

用dp[x]表示装前x个的最小费用，sum[x]表示C的前缀和。

可以发现dp[i]=min{dp[j]+(i-j+sum[i]-sum[j]-1-L)^2} (0<=j<i)

这样似乎还是不够美观，我们令p[i]=i+sum[i]，g=L+1。

dp[i]=min{dp[j]+(p[i]-p[j]-g)^2} (0<=j<i)

美观了一点…

这样硬肛是O(n^2)的，感觉很不兹磁啊…

首先：四边形不等式

当函数w(i,j)满足w(a,c)+w(b,d)<=w(b,c)+w(a,d)且a<=b<c<=d时我们称w(i,j)满足四边形不等式。

假如我们用w(j,i)表示(p[i]-p[j]-g)^2，那么（打表）可以发现w是满足四边形不等式的。

什么？讲道理？

w(a,c)+w(b,d)-w(b,c)-w(a,d)=2g(p[c]-p[a]+p[d]-p[b]-p[c]+p[b]-p[d]+p[a])+p[a]^2+p[c]^2+p[b]^2+p[d]^2-p[b]^2-p[c]^2-p[a]^2-p[d]^2-2p[a]p[c]-2p[b]p[d]+2p[b]p[c]+2p[a]p[d]（展开）=-2p[a]p[c]-2p[b]p[d]+2p[b]p[c]+2p[a]p[d]（容易观察出剩下的都为0）=2(p[d]-p[c])(p[a]-p[b])<0（由于p显然单调增）。

模型一 且w满足四边形不等式

由于决策单调性，我们可以知道如果a<b<c<d且在c处选a比选b优，那么在d处选a也比选b优。

所以我们可以用一个单调队列（单调栈）来维护决策，每有一个新决策我们就用二分维护队列最优性，队列每一个元素维护对于哪些状态（一定是一个连续的区间）当前这个决策时最优的，然后队列从尾到头一个一个元素二分当前状态哪里最优，然后暴力弹出就行。

#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include <algorithm>
using namespace std;
typedef long long ll;
#define SZ 233333
int n,l; ll p[SZ],dp[SZ];
int sn=0,sa[SZ],sl[SZ],sr[SZ];
ll wd(int j,int i) {return dp[j]+(p[i]-p[j]-l)*(p[i]-p[j]-l);}
int main()
{
    scanf("%d%d",&n,&l); ++l;
    ll sum=0;
    for(int i=1;i<=n;i++)
    {
        int c; scanf("%d",&c);
        sum+=c; p[i]=sum+i;
    }
    sn=1; sa[1]=0; sl[1]=1; sr[1]=n;
    for(int i=1;i<=n;i++)
    {
        int jc=sa[upper_bound(sl+1,sl+1+sn,i)-sl-1];
        dp[i]=wd(jc,i);
        while(sn&&wd(sa[sn],sl[sn])>=wd(i,sl[sn])) --sn;
        if(!sn) {sn=1; sa[1]=i; sl[1]=1; sr[1]=n; continue;}
        int l=sl[sn],r=sr[sn]; //到l为止原决策更优
        while(l<r)
        {
            int mid=l+r+1>>1;
            if(wd(sa[sn],mid)<wd(i,mid)) l=mid; else r=mid-1;
        }
        if(l==n) continue;
        sr[sn]=l; ++sn; sa[sn]=i;
        sl[sn]=l+1; sr[sn]=n;
    }
    printf("%lld\n",dp[n]);
}

愉快的O(nlogn)。

②土地购买 bzoj1597

购买一些土地，可以分组购买，每组土地的价格是最大长*最大宽，求最小费用。

例如1*5和5*1两块地显然要分2组购买。

我们考虑把长度从高到低排个序，这样我们就只要考虑宽度就行啦。

我们用l表示长度，w表示宽度好了，那么

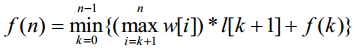
我们发现这个玩意儿根本不满足决策单调性…

我们回想一下之前做的某一题（其实我也忘了是哪一题），只要把完全没有用，会被完全包含的点删掉就是单调的了。

我们发现如果点(l,w)存在另一个点(l',w')且l<=l'，w<=w'，那么(l,w)一定可以在选(l',w')的时候被顺便选掉，不会影响总代价。

我们考虑先将l排好序后，用一个单调栈一样的东西来维护一下w，显然是线性的。

之后的方程就是单调的了。

（这里我们改用x表示长度，y表示宽度，懒得改公式了）

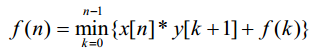
还是可以像上一题一样讲道理！

我们令w(k,n)为x[n]*y[k+1]，那么

w(a,c)+w(b,d)-w(b,c)-w(a,d)=(x[b]-x[a])*(y[d+1]-y[c+1])。

由于x不减y不增显然<=0。

#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include <algorithm>
using namespace std;
#define X first
#define Y second
#define SZ 666666
typedef pair<int,int> pii;
typedef long long ll;
pii ps[SZ];
int n,sn=0,ss[SZ];
bool dd[SZ];
ll dp[SZ];
int jn=0,jl[SZ],jr[SZ],jc[SZ],nxt[SZ];
ll w(int a,int b) {return ps[b].X*(ll)ps[nxt[a]].Y+dp[a];}
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++) scanf("%d%d",&ps[i].X,&ps[i].Y);
    sort(ps+1,ps+1+n);
    for(int i=1;i<=n;i++)
    {
        while(sn&&ps[ss[sn]].Y<=ps[i].Y) dd[ss[sn--]]=1;
        ss[++sn]=i;
    }
    jn=1; jc[1]=0; jl[1]=1; jr[1]=n;
    int lst=0;
    for(int i=1;i<=n;i++)
    {
        if(!dd[i]) nxt[lst]=i, lst=i;
    }
    for(int i=1;i<=n;i++)
    {
        if(dd[i]) continue;
        int t=upper_bound(jl+1,jl+1+jn,i)-jl-1;
        dp[i]=w(jc[t],i);
        while(jn&&w(jc[jn],jl[jn])>=w(i,jl[jn])) --jn;
        if(!jn) {jn=1; jc[1]=i; jl[1]=1; jr[1]=n; continue;}
        int l=jl[jn],r=jr[jn];
        while(l<r)
        {
            int mid=l+r+1>>1;
            if(w(jc[jn],mid)<w(i,mid)) l=mid; else r=mid-1;
        }
        if(l==n) continue;
        jr[jn]=l; ++jn; jc[jn]=i;
        jl[jn]=l+1; jr[jn]=n;
    }
    printf("%lld\n",dp[n]);
}

模型二，即单调队列优化

这个最典型的就是有限背包（多重背包）

比如我们有若干个物品，价值为v[i]，重量为w[i]，数量限制为s[i]。

我们考虑一个傻逼dp：

f[i][j]=max{f[i-1][j-x*w[i]]+x*v[i]} (0<=x<=s[i]，x*w[i]<=j)

然后我们发现这个x*w[i]<=j不太和谐…

我们考虑把j对模w[i]的余数进行分类！

设j=q*w[i]+p，那么

f[i][p][q]=max{f[i-1][p][x]+(q-x)*v[i]} (0<=x<=q且x>=q-s[i]）

所以我们发现可以直接上单调队列优化！

就是说我们可以用一个单调队列来维护决策，队伍里前面的决策比后面的一定优秀。

每一次我们在队尾加新的决策，然后维护队列的单调性。

#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include <memory.h>
using namespace std;
#define SZ 666666
int n,tw;
typedef long long ll;
ll f[SZ];
void pack01(ll w,ll v)
{
    for(int i=tw;i>=w;i--) f[i]=max(f[i],f[i-w]+v);
}
void packfull(ll w,ll v)
{
    for(int i=w;i<=tw;i++) f[i]=max(f[i],f[i-w]+v);
}
//强行二进制分解
void packmulti2(ll w,ll v,int c)
{
    if(w>tw||c==0) return;
    if(c==1) {pack01(w,v); return;}
    if(w*c>=tw) {packfull(w,v); return;}
    for(int k=1;k<c;k<<=1) pack01(w*k,v*k), c-=k;
    pack01(w*c,v*c);
}
int qs[SZ],*qh[SZ],*qt[SZ];
ll nf[SZ];
//据说比较优越的单调队列
void packmulti1(ll w,ll v,int c)
{
    if(w>tw||c==0) return;
    if(c==1) {pack01(w,v); return;}
    if(w*c>=tw) {packfull(w,v); return;}
    int pss=tw/w+1,*cur=qs;
    for(int i=0;i<w;i++) qh[i]=qt[i]=cur, cur+=pss;
    for(int i=0;i<=tw;i++)
    {
        int bl=i%w; ll cv=f[i]-i/w*v;
        while(qh[bl]!=qt[bl]&&*qh[bl]<i-c*w) ++qh[bl];
        while(qh[bl]!=qt[bl]&&f[*(qt[bl]-1)]-*(qt[bl]-1)/w*v<cv) --qt[bl];
        *(qt[bl]++)=i;
        nf[i]=f[*qh[bl]]+(i/w-(*qh[bl])/w)*v;
    }
    for(int i=0;i<=tw;i++) f[i]=nf[i];
}
int main()
{
    scanf("%d%d",&n,&tw);
    for(int i=1;i<=n;i++)
    {
        int w,v,m;
        scanf("%d%d%d",&w,&v,&m);
        if(m==1) pack01(w,v);
        else if(m==-1) packfull(w,v);
        else packmulti2(w,v,m);
    }
    printf("%lld\n",f[tw]);
}

不知道是不是我写狗了…单调队列做法跑的特别慢…一脸懵逼