[POJ1765]November Rain

[POJ1765]November Rain

试题描述

Contemporary buildings can have very complicated roofs. If we take a vertical section of such a roof it results in a number of sloping segments. When it is raining the drops are falling down on the roof straight from the sky above. Some segments are completely exposed to the rain but there may be some segments partially or even completely shielded by other segments. All the water falling onto a segment as a stream straight down from the lower end of the segment on the ground or possibly onto some other segment. In particular, if a stream of water is falling on an end of a segment then we consider it to be collected by this segment.

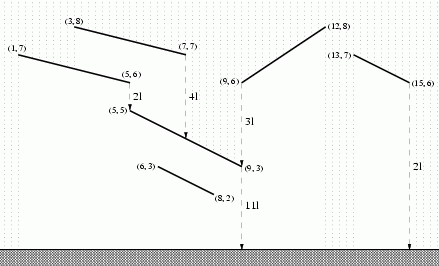
For the purpose of designing a piping system it is desired to compute how much water is down from each segment of the roof. To be prepared for a heavy November rain you should count one liter of rain water falling on a meter of the horizontal plane during one second.

Task 
Write a program that:

reads the description of a roof, 
computes the amount of water down in one second from each segment of the roof, 
writes the results.

输入

The first line of the input contains one integer n (1 <= n < = 40000) being the number of segments of the roof. Each of the next n lines describes one segment of the roof and contains four integers x1, y1, x2, y2 (0 <= x1, y1, x2, y2 < = 1000000, x1 < x2, y1<>y2) separated by single spaces. Integers x1, y1 are respectively the horizontal position and the height of the left end of the segment. Integers x2, y2 are respectively the horizontal position and the height of the right end of the segment. The segments don't have common points and there are no horizontal segments. You can also assume that there are at most 25 segments placed above any point on the ground level.

输出

The output consists of n lines. The i-th line should contain the amount of water (in liters) down from the i-th segment of the roof in one second.

输入示例

输出示例

数据规模及约定

见“输入”

题解

注意到每个竖直线上的交点不会超过 25 个，我们可以用扫描线后暴力乱搞。

每遇到一个屋檐的左端点就插入，遇到右端点就删除，在每次删除后处理天降雨的情况，即把最上面的屋檐集水量增加。

然后对于斜率为正的线段的左端点向下找到最靠近的一个屋檐向其连边，对于斜率为负的线段右端点同理。这样我们就可以得到一个 DAG，按拓扑序依次往后累加就好了（可以理解成 dp）。

这题有点卡常，需要离散一下。

#include <iostream>
#include <cstdio>
#include <cstdio>
#include <cstring>
#include <cctype>
#include <algorithm>
#include <cmath>
using namespace std;

int read() {
	int x = 0, f = 1; char c = getchar();
	while(!isdigit(c)){ if(c == '-') f = -1; c = getchar(); }
	while(isdigit(c)){ x = x * 10 + c - '0'; c = getchar(); }
	return x * f;
}

#define maxn 40010
#define maxx 1000010
#define maxm 40010
#define eps 1e-6
int n, ca, cm, f[maxn];
struct Line {
	int x1, y1, x2, y2;
	double slop;
	Line() {}
	Line(int _1, int _2, int _3, int _4, double _5): x1(_1), y1(_2), x2(_3), y2(_4), slop(_5) {}
} ls[maxn];
struct Point {
	double x, h, slop;
	int id;
	Point() {}
	Point(double _1, double _2, double _3, int _4): x(_1), h(_2), slop(_3), id(_4) {}
	bool operator < (const Point& t) const { return fabs(h - t.h) <= eps ? 0 : h < t.h; }
} ad[maxn], mi[maxn], tmp[30], ae[30];
bool cmp(Point a, Point b) { return a.x < b.x; }

int m, head[maxn], to[maxm], next[maxm], ind[maxn], lst[maxn], cl;
void AddEdge(int a, int b) {
//	printf("edge: %d -> %d\n", a, b);
	to[++m] = b; next[m] = head[a]; head[a] = m;
	ind[b]++;
	return ;
}

int vis[maxn], num[maxn<<1], cnt, A[maxn<<1];
int main() {
	n = read();
	for(int i = 1; i <= n; i++) {
		int x1 = read(), y1 = read(), x2 = read(), y2 = read();
		double slop = (double)(y2 - y1) / (x2 - x1);
		ls[i] = Line(x1, y1, x2, y2, slop);
		num[++cnt] = x1; num[++cnt] = x2;
	}
	sort(num + 1, num + cnt + 1);
	cnt = unique(num + 1, num + cnt + 1) - num - 1;
	for(int i = 1; i < cnt; i++) A[i] = num[i+1] - num[i];
	for(int i = 1; i <= n; i++) {
		ls[i].x1 = lower_bound(num + 1, num + cnt + 1, ls[i].x1) - num;
		ls[i].x2 = lower_bound(num + 1, num + cnt + 1, ls[i].x2) - num;
		ad[++ca] = Point(ls[i].x1, ls[i].y1, ls[i].slop, i);
		mi[++cm] = Point(ls[i].x2, ls[i].y2, ls[i].slop, i);
	}
	sort(ad + 1, ad + ca + 1, cmp);
	sort(mi + 1, mi + cm + 1, cmp);

	memset(vis, -1, sizeof(vis));
	int ka = 1, km = 1, kt = 0;
	for(int i = 1; i <= cnt; i++) {
		for(int j = 1; j <= kt; j++) tmp[j].h += tmp[j].slop * A[i-1];
		int ke = 0;
		while(ad[ka].x == i) {
			if(ad[ka].slop > 0.0) ae[++ke] = ad[ka];
			tmp[++kt] = ad[ka];
			ka++;
		}
		sort(tmp + 1, tmp + kt + 1);
		for(int j = 1; j <= ke; j++) {
			int k = lower_bound(tmp + 1, tmp + kt + 1, Point(-1, ae[j].h, -1, -1)) - tmp;
			if(k == 1) continue; k--;
			AddEdge(ae[j].id, tmp[k].id);
		}
//		for(int j = 1; j <= kt; j++) printf("%d ", tmp[kt].id); putchar('\n');
		ke = 0;
		while(mi[km].x == i) {
			if(mi[km].slop < 0.0) ae[++ke] = mi[km];
			vis[mi[km].id] = i;
			km++;
		}
//		for(int j = 1; j <= kt; j++) printf("%d: %.2lf\n", tmp[j].id, tmp[j].h);
		for(int j = 1; j <= ke; j++) {
			int k = lower_bound(tmp + 1, tmp + kt + 1, Point(-1, ae[j].h, -1, -1)) - tmp;
//			if(ae[j].id == 5) printf("here!!! %d %.2lf\n", k, ae[j].h);
			if(k == 1) continue; k--;
			AddEdge(ae[j].id, tmp[k].id);
		}
		for(int k = 1; k <= kt; k++)
			if(vis[tmp[k].id] == i) {
				swap(tmp[k], tmp[kt]);
				kt--; k--;
			}
		sort(tmp + 1, tmp + kt + 1);
		f[tmp[kt].id] += A[i];
//		printf("add_id: %d %d\n", tmp[kt].id, A[i]);
	}

	for(int i = 1; i <= n; i++) if(!ind[i]) lst[++cl] = i;
	int i = 1;
	for(; i <= cl; i++)
		for(int e = head[lst[i]]; e; e = next[e]) {
			ind[to[e]]--;
			if(!ind[to[e]]) lst[++cl] = to[e];
		}
	for(int i = 1; i <= n; i++) {
		int u = lst[i];
		for(int e = head[u]; e; e = next[e])
			f[to[e]] += f[u];
	}

	for(int i = 1; i <= n; i++) printf("%d\n", f[i]);

	return 0;
}