学C记录（理解递归问题之汉诺塔）

汉诺游戏规则如下：

1、有三根相邻的柱子，标号为A,B,C。

2、A柱子上从下到上按金字塔状叠放着n个不同大小的圆盘。

3、现在把所有盘子一个一个移动到柱子B上，并且每次移动同一根柱子上都不能出现大盘子在小盘子上方。

程序要求：

输入盘子个数，输出完成步骤。

解决思路：

在完成题目前，首先应对游戏规则和解题方法有所了解，此处借7k7k小游戏中的汉诺塔（3个）演示。

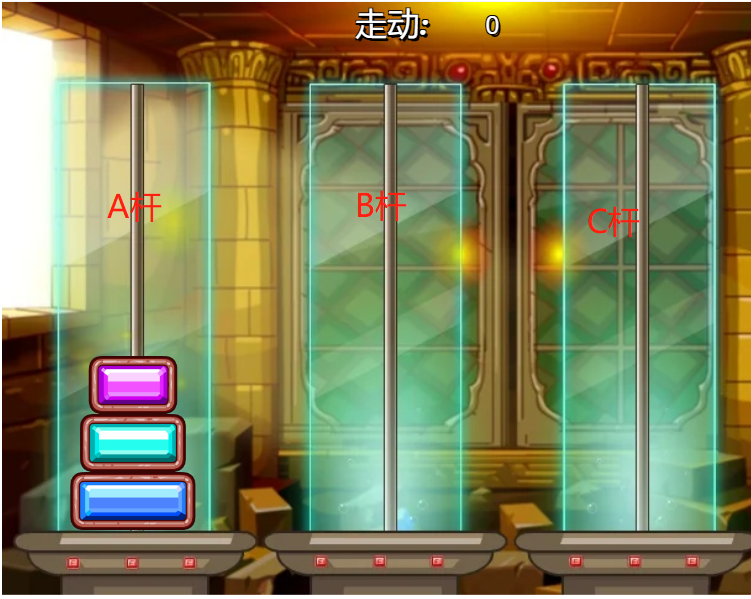
首先我们的目的是把A的三个盘子移到C处，所以首先应完成的便是把上两个盘子放到B上，才能把第三个（最大的）盘子放到C，接着把B上的两个放到C上。

所以这时我们发现，B的作用便是用来暂时存放除了最后一个的其他所有盘子，以便后续操作

所以我们可以设置x，y，z三个变量，分别表示初始盘子的位置，借放盘子的位置，最终完成的位置。

注意：x，y，z不一定与A，B，C始终一一对应！！！

A，B，C只是杆的名字！！！

因此程序的步骤：

1.当盘子等于一个，直接由x移到z。

2.当盘子大于一个（假设n个），先把n-1个盘子移到y，把第n个也就是最后一个大的，移到z。

3.把y上的盘子移到z。

刚开始我们把A，B，C对应x，y，z

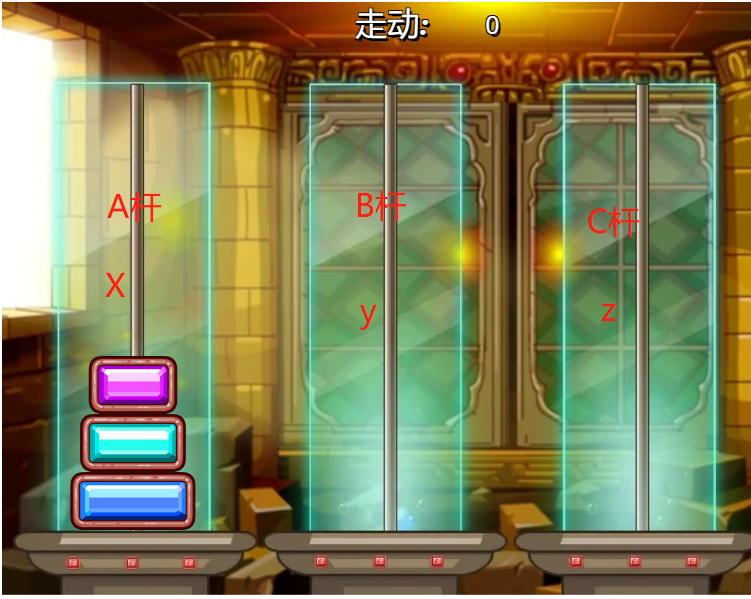
这时有个问题怎么把x上的盘子移到y呢，这时我们就要转换一下，先忽略掉第三个最大的盘的存在，把B杆看成目的地，C杆就变成y了（这就是为什么说ABC与xyz不是一定对应的原因）

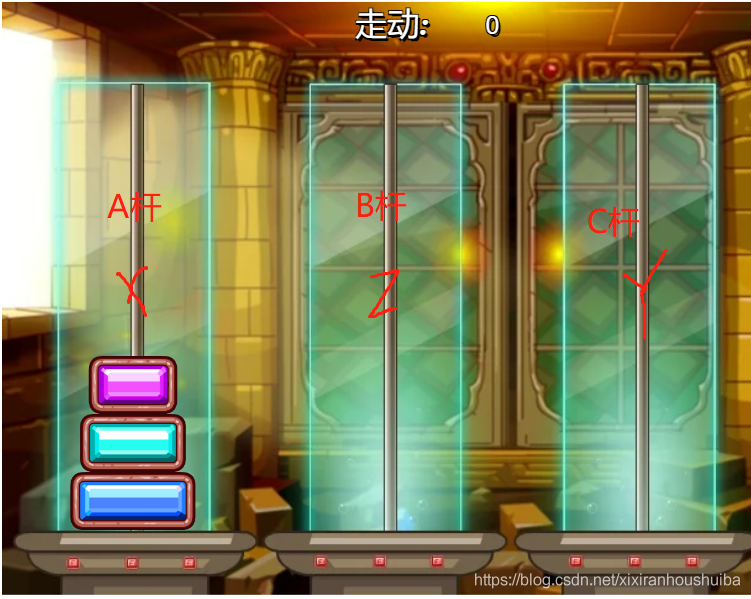
完成了上两个转移到B杆，便可以把A杆的最大盘移到C

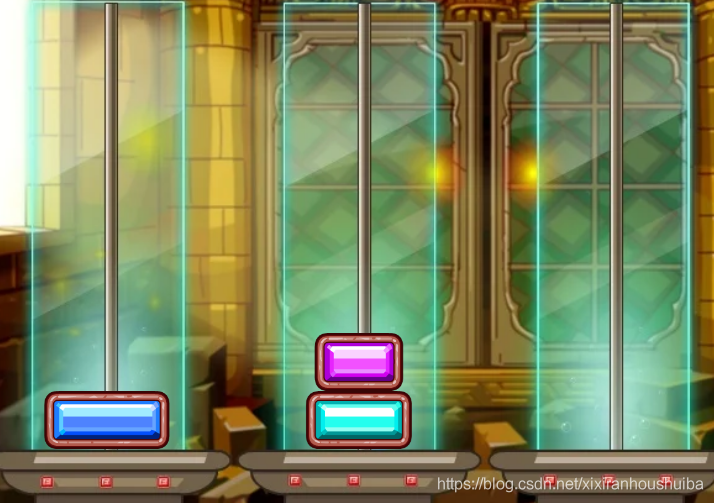
但当我们完成步骤2时，我们可以把原来的y也就是b杆看成是x（初始放盘子的地方），A杆看成y，C杆看成z（目的地），这时候便于刚开始步骤相似了

{{uploading-image-916509.png(uploading...)}}

所以重要的便是对盘子个数的判断和对xyz的转换

所以可以动手写代码了，如下：

void Hanoi(int n, char x, char y, char z) //n为盘子个数
 {
	void move(char x, char z);
	if (1 == n)//当n等于1，执行步骤1
	 {
		move(x, z);
	}
	else //当n不等于1，执行步骤2
	{
		Hanoi(n - 1, x, z, y);//把n-1从x移到y，所以原来的z便是现在借放的y，y同，所以反过来
		Hanoi(1, x, y, z);//完成上一步x移到上一步的y，就把最后的第n个从x移到z
		Hanoi(n - 1, y, x, z);//（此时的y有n-1个盘子，看成初始位置x），目的地还是z
	}
}

所以通过上面的操作便完成了盘子的所有移到

move函数的定义：

void move(char x, char z)
{
	printf("%c ---> %c \n", x, z);
}

所以整个程序的代码如下：

int main() {
	int n = 0;
	void Hanoi(int n, char x, char y, char z);
	printf("请输入所要移动的盘子的个数：");
	scanf("%d", &n);
	Hanoi(n, 'A', 'B', 'C');
}

void Hanoi(int n, char x, char y, char z)
{
	void move(char x, char z);
	if (1 == n) {
		move(x, z);
	} else {
		Hanoi(n - 1, x, z, y);
		Hanoi(1, x, y, z);
		Hanoi(n - 1, y, x, z);
	}
}

void move(char x, char z)
{
	printf("%c ---> %c \n", x, z);
}