详解递归（基础篇）———函数栈、阶乘、Fibonacci数列

一、递归的基本概念

递归函数:在定义的时候，自己调用了自己的函数。

注意：递归函数定义的时候一定要明确结束这个函数的条件！

二、函数栈

栈:一种数据结构，它仅允许栈顶进，栈顶出，先进后出，后进先出。我们可以简单的理解为栈就是一个杯子，这个杯子里面有很多隔层，每一层都可以放东西，第一个放入的东西就在杯子最后一层，第二个放入的东西就在倒数第二层，现在我们要取出最后一层的东西，就必须先把第二层的东西给出来。

函数栈：栈里面每一层都是装的都是函数的栈就是函数栈，调用一个函数的时候，这个函数就入栈，这个函数调用完成了（执行到了函数的最后一个语句或者说return了），就出栈。

下面是一个演示函数栈运行机制的C语言程序，并无实际意义，仅用于理解函数栈：

#include<stdio.h>

void function1()
{
    printf("function1 done!")
    return;     //第三步，函数function1调用完毕，出栈
}
void function2()
{
    printf("function2 done!")
    return;     //第五步，函数function2调用完毕，出栈
}
void function3()
{
    printf("function3 done!")
    return;     //第八步，函数function3调用完毕，出栈
}
void function4()
{
    printf("function4 done!")
    function3();    //第七步，调用函数function3，入栈
    return;         //第九步，函数function4调用完成,出栈
}

int main()//第一步，调用主函数，主函数入栈（这个C语言程序的入口）
{
    function1();    //第二步，调用函数function1，入栈
    function2();    //第四步，调用函数function2，入栈
    function4();    //第六步，调用函数function4，入栈
    return 0;       //第十步，主函数调用完成，出栈（整个程序执行完成）
}

三、实例

1、阶乘

题目：用递归方法实现计算整数n的阶乘n!

解析：

首先，我们易知0！=1； 1！=1； 2！=2*1！； 3！=3*2！； 4！=4*3！；……

那么我们可以得到递推公式

• n!=1[n=0,1]
• n!=n*(n-1)![n>=2]

从而我们就可以写出计算阶乘的递归程序的C语言代码，如下：

#include<stdio.h>

long Fact(int n);

int main()
{
    int n;
    long result;
    printf("Input n:");
    scanf("%d",&n);
    result = Fact(n);
    if(result == -1)
        printf("n<0,data error!\n");
    else
        printf("%d! = %ld\n", n, result);
    return 0;
}

long Fact(int n)
{
     //对传入函数的值判断其合法性
    if(n < 0)
    {
        return -1;
    }
    //计算n的阶乘的表达式改写的代码
    else if(n == 0 || n == 1)
    {
        return 1;
    }
    else
    {
        return (n*Fact(n-1));
    }
}

当然，写出来了并不代表我们理解，下图讲解了在这个程序中是如何计算4的阶乘的。

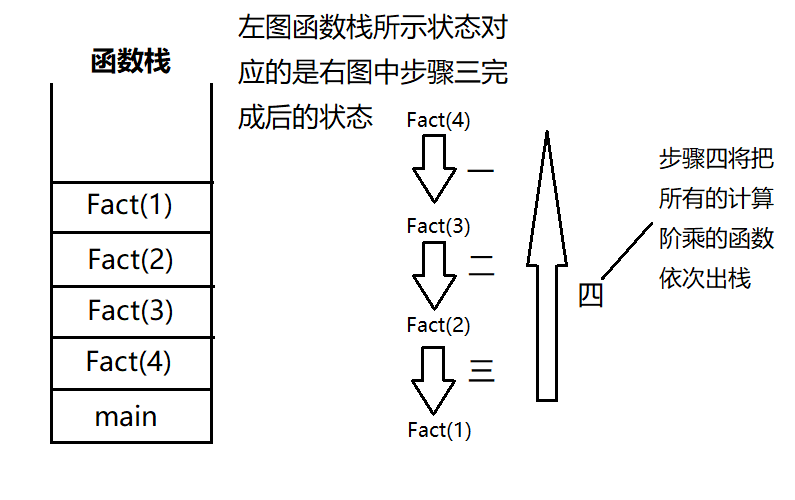
2、Fibonacci数列

题目：实现函数表达式Fib(0)=0,Fib(1)=1,Fib(n)=Fib(n-1)+Fib(n-2)。

解析：在这里题目已经给出了递归表达式，那么我们可以轻松地写出C语言代码。

#include<stdio.h>

int Fib(int n)
{
    //判断传入数据的合法性
    if(n < 0)
    {
        return -1;
    }

    //递归表达式改而写的C语言代码
    else if(n == 0)
    {
        return 0;
    }
    else if(n == 1)
    {
        return 1;
    }
    else
    {
        return Fib(n-1)+Fib(n-2);
    }
}

int main()
{
    int n,result;
    printf("Input n:");
    scanf("%d",&n);
    result = Fib(n);
    if(result == -1)
    {
        printf("A illegal data!");
    }
    else
    {
        printf("Fib(%d) = %d", n, result);
    }
    return 0;
}

关于用Fibonacci数列的在上述程序中如何计算的，我们仍然是通过函数栈进行，具体如何运行在此就不再赘述。