DeepFool: a simple and accurate method to fool deep neural networks

概
主要内容
- 二分类模型
  - 为线性
  - 为一般二分类
- 多分类问题
  - 仿射
  - 为一般多分类

Moosavidezfooli S, Fawzi A, Frossard P, et al. DeepFool: A Simple and Accurate Method to Fool Deep Neural Networks[C]. computer vision and pattern recognition, 2016: 2574-2582.

@article{moosavidezfooli2016deepfool:,

title={DeepFool: A Simple and Accurate Method to Fool Deep Neural Networks},

author={Moosavidezfooli, Seyedmohsen and Fawzi, Alhussein and Frossard, Pascal},

pages={2574--2582},

year={2016}}

概

本文从几何角度介绍了一种简单而有效的方法.

主要内容

adversarial的目的:

\[\tag{1}
\Delta(x;\hat{k}):= \min_{r} \|r\|_2 \: \mathrm{subject} \: \mathrm{to} \: \hat{k}(x+r) \not = \hat{k}(x),
\]

其中$\hat{k}(x)$为对$x$的标签的一个估计.

二分类模型

当模型是一个二分类模型时,

\[\hat{k}(x) = \mathrm{sign}(f(x)),
\]

其中$f:\mathbb{R}^n \rightarrow \mathbb{R}$为分类器, 并记$\mathcal{F}:= \{x: f(x)=0\}$为分类边界.

$f$为线性

即$f(x)=w^Tx+b$:

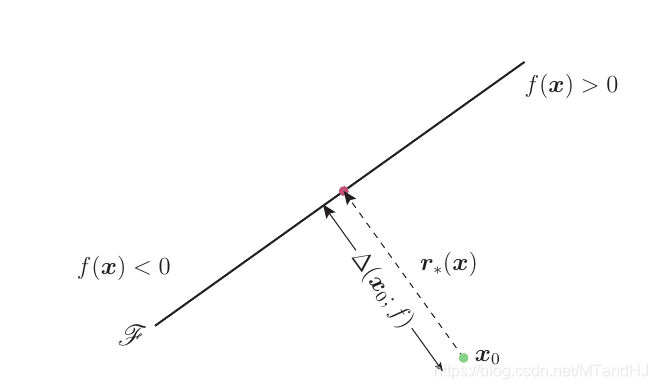
假设$x_0$在$f(x)>0$一侧, 则

\[r_*(x_0)= -\frac{f(x_0)}{\|w\|_2^2}w.
\]

$f$为一般二分类

此时, 我们$f$的一阶近似为

\[f(x_0+r)\approx f(x_0)+\nabla^T f(x_0) r,
\]

此时分类边界为$\mathcal{F} =\{x:f(x_0)+\nabla^T f(x_0) (x-x_0)=0\}$,此时$w=\nabla f(x_0),b=f(x_0),$ 故

\[\tag{4}
r_*(x_0) \approx -\frac{f(x_0)}{\|\nabla f(x_0)\|_2^2} \nabla f(x_0).
\]

所以, 每次

\[r_i = -\frac{f(x_i)}{\|\nabla f(x_i)\|_2^2} \nabla f(x_i), \\
x_{i+1} = x_i+r_i,
\]

直到$\hat{k}(x_i) \not= \hat{k}(x_0)$是停止, 算法如下

多分类问题

$f:\mathbb{R}^n \rightarrow \mathbb{R}^c$, 此时

\[\tag{5}
\hat{k}(x) = \arg \max_k f_k(x).
\]

$f$仿射

即$f(x) = W^Tx + b$, 设$W$的第$k$行为$w_k$,

\[\tag{7}
P=\cap_{k=1}^c \{x: f_{\hat{k}(x_0)}(x) \ge f_k(x)\},
\]

为判定为$\hat{k}(x_0)$的区域, 则$x+r$应落在$P^{c}$, 而

\[\Delta (x_0;f)= \mathbf{dist} (x_0, P^c).
\]

当$f$为仿射的时候, 实际上就是找$x_0$到各分类边界(与$x_0$有关的)最短距离,

\[\tag{8}
\hat{l}(x_0) = \arg \min _{k \not = \hat{k}(x_0)} \frac{|f_k(x_0) - f_{\hat{k}(x_0)}(x_0)|}{\|w_k-w_{\hat{k}(x_0)}\|_2},
\]

则

\[\tag{9}
r_*(x_0)= \frac{|f_{\hat{l}(x_0)}(x_0) - f_{\hat{k}(x_0)}(x_0)|}{\|w_{\hat{l}(x_0)}-w_{\hat{k}(x_0)}\|_2^2}(w_{\hat{l}(x_0)}-w_{\hat{k}(x_0)}),
\]

$f$为一般多分类

\[\tag{10}
\tilde{P}_i=\cap_{k=1}^c \{x: f_{\hat{k}(x_0)}(x_i) + \nabla^T f_{\hat{k}(x_0)}(x_i) (x-x_i)\ge f_k(x_i) + \nabla^Tf_k(x_i)(x-x_i)\},
\]

则

\[r_i(x_i)=\frac{|f_{\hat{l}(x_i)}(x_i) - f_{\hat{k}(x_0)}(x_i)|}{\|\nabla f_{\hat{l}(x_i)}(x_i) - \nabla f_{\hat{k}(x_0)}(x_i)\|_2^2}(\nabla f_{\hat{l}(x_i)}(x_i) - \nabla f_{\hat{k}(x_0)}(x_i)).
\]

$l_p$

$p \in (1, \infty)$的时候

考虑如下的问题

\[\begin{array}{ll}
\min & \|r\|_p^p \\
\mathrm{s.t.} & w^T(x+r)+b=0,
\end{array}
\]

利用拉格朗日乘子

\[\min_r \: \|r\|_p^p + c(w^T(x+r)+b),
\]

由KKT条件可知(这里的$r_k$表示第$k$个元素)

\[p\: |r_k|^{p-1} = c_kw_k,
\]

注: 这里有一个符号的问题, 但是可以把符号放入$c_k$中进而不考虑,

故

\[r_*= c \odot w^{q-1},
\]

其中$q=\frac{p}{p-1}$为共轭指数, 并$c=[c_1,\ldots]^T$,且$|c_i|=|c_j|,$ 记$w^{q-1}=[|w_1|^{q-1},\ldots]^T$,又

\[w^T(x+c\odot w^{q-1})+b=0,
\]

故

\[|c|=\frac{|w^Tx+b|}{\|w\|_q^q} ,
\]

故

\[r_*=-\frac{w^Tx+b}{\|w\|_q^q} w^{q-1} \odot \mathrm{sign}(w).
\]

$p=1$, 设$w$的绝对值最大的元素为$w_{m}$, 则

\[r_*=-\frac{w^Tx+b}{w_m} \mathrm{1}_m,
\]

$\mathrm{1}_m$为第$m$个元素为1, 其余元素均为0的向量.

$p=\infty$,

\[r_*=-\frac{|w^Tx+b|}{\|w\|_1} \mathrm{sign} (w).
\]

故:

$p \in [1, \infty)$:

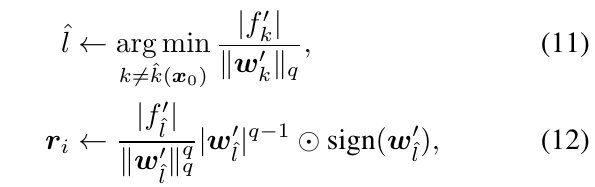
$p=\infty$:

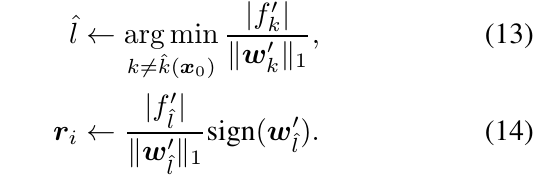
注: 因为, 仅仅到达边界并不足够, 往往希望更进一步, 所以在最后(?)$x=x+ (1+\eta) r$, 文中取$\eta=0.02$.