洛谷P1002过河卒java100分题解

题目描述如图：

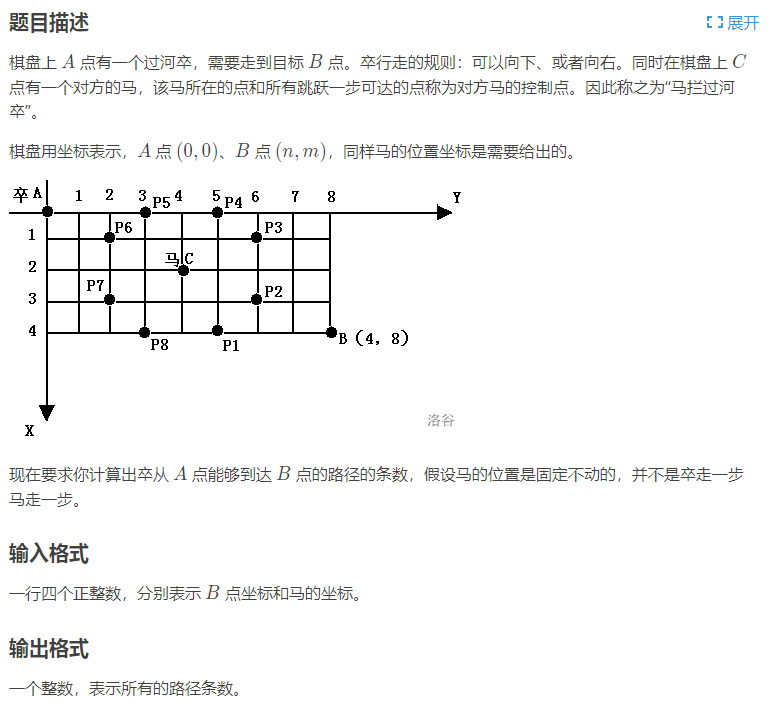
这道题我以前以回溯的方法做，只能拿到60分

现在才发现是道动态规划题

解题思路：

创建一个(0,0)到终点打小的二维数组表示棋盘

每个坐标的值为此位置到终点的路数

最下方一排和最右方一列如果没有马的控制点，能到终点的路数为1

如图所示：

从下向上，从右向左遍历，每个格子到终点的路数等于下方的格子的值+右方的格子的值

如果遇到马的控制点，则不计算这个格子

完整代码如下：

import java.util.Scanner;

public class DP1 {
    public static void main(String[] args) {
        Scanner sc=new Scanner(System.in);
        //创建棋盘
        int a=sc.nextInt();
        int b=sc.nextInt();
        a++;
        b++;
        long[][] qp=new long[a][b];

        //创建马
        int n=sc.nextInt();
        int m=sc.nextInt();

        //如果马的控制点在棋盘内 设置为0
        qp[n][m]=-1;
        if (n-1>=0&&m-2>=0){
            qp[n-1][m-2]=-1;
        }
        if (n-1>=0&&m+2<b){
            qp[n-1][m+2]=-1;
        }
        if (n-2>=0&&m-1>=0){
            qp[n-2][m-1]=-1;
        }
        if (n-2>=0&&m+1<b){
            qp[n-2][m+1]=-1;
        }
        if (n+1<a&&m-2>=0){
            qp[n+1][m-2]=-1;
        }
        if (n+1<a&&m+2<b){
            qp[n+1][m+2]=-1;
        }
        if (n+2<a&&m-1>=0){
            qp[n+2][m-1]=-1;
        }
        if (n+2<a&&m+1<b){
            qp[n+2][m+1]=-1;
        }

        //将棋盘下方边和右方边初始化为1
        for (int i = a-1; i>=0; i--) {
            if (qp[i][b-1]==-1){
                break;
            }
            qp[i][b-1]=1;
        }
        for (int i = b-1; i >=0; i--) {
            if (qp[a-1][i]==-1){
                break;
            }
            qp[a-1][i]=1;
        }

        for (int i = a-2; i >= 0; i--) {
            for (int j = b-2; j >= 0; j--) {
                if (qp[i][j]==-1){
                    continue;
                }
                if (qp[i+1][j]==-1&&qp[i][j+1]==-1){
                    continue;
                }
                if (qp[i+1][j]<0){
                    qp[i][j]=qp[i][j+1];
                    continue;
                }
                if (qp[i][j+1]<0){
                    qp[i][j]=qp[i+1][j];
                    continue;
                }
                qp[i][j]=qp[i+1][j]+qp[i][j+1];
            }
        }
        System.out.println(qp[0][0]);

    }
}