Codeforces gym 101343 A. On The Way to Lucky Plaza【概率+逆元+精度问题】

 2017 JUST Programming Contest 2.0

题目链接：http://codeforces.com/gym/101343/problem/A

A. On The Way to Lucky Plaza

time limit per test：1.0 s

memory limit per test：256 MB

input：standard input

output：standard output

Alaa is on her last day in Singapore, she wants to buy some presents to her family and friends. Alaa knows that the best present in the world will be a chocolate plate for each one of her family members and friends.

Alaa goes to Lucky Plaza shopping mall in Orchard road in order to find all chocolate she needs. Lucky Plaza is a big mall and have many shops that sell chocolate.

On the entrance of Lucky Plaza Alaa wondered if she wants to buy k chocolate plates, what is the probability that she will buy the k^th chocolate plate from the n^th shop she will visit, knowing that she can visit each shop at most one time. Also she can buy at most one chocolate plate from each shop, and the probability to do that is p. (This probability is the same for all shops in Lucky Plaza)

Alaa wants to finish her mission as soon as possible, so she starts visiting the shops, also she asked you to calculate the answer of her hard question. Can you?

Input

The first line contains three integers m, n, k and real number p (1  ≤  m, n, k  ≤  10⁵) (0  ≤  p  ≤  1), where m is the number of shops that sell chocolate in Lucky Plaza, n is the number of shops Alaa will visit, k is the number of chocolate plates Alaa wants to buy, and p is the probability that Alaa will buy a chocolate plate from any shop that sell chocolate.

The probability p is given with exactly three digits after the decimal point

Output

On a single line print y, where y is the sought probability computed modulo 10⁹ + 7.

The answer y is defined precisely as follows. Represent the probability that Alaa will buy the k^th chocolate plate from the n^th shop she will visit as an irreducible fraction p / q. The number y then must satisfy the modular equation y × q ≡ p (mod 10⁹ + 7), and be between 0 and 10⁹ + 6, inclusive. It can be shown that under the constraints of this problem such a number y always exists and is uniquely determined.

Examples

Input

5 1 1 0.500

Output

500000004

Input

9 4 2 0.800

Output

417600003

Input

100 5 5 0.200

Output

714240005

Note

In the first test case there are 5 shops that sell chocolate in Lucky Plaza, and Alaa wants to buy only 1 chocolate plate. In this case Alaa wants to know what is the probability that she will buy the 1^st chocolate plate from the 1^st shop she will visit. The probability is 1 / 2, and the answer is 500000004, since (500000004 * 2) % (10⁹ + 7) = 1 % (10⁹ + 7).

In the second test case there are 9 shops that sell chocolate in Lucky Plaza, and Alaa wants to buy only 2 chocolate plates. In this case Alaa wants to know what is the probability that she will buy the 2^nd chocolate plate from the 4^th shop she will visit. The probability is 48 / 625, and the answer is 417600003, since (417600003 * 625) % (10⁹ + 7) = 48 % (10⁹ + 7).

题意：去m个超市买东西，在每个超市买东西的概率都为p，并且最多只能买一件。求在第n个超市刚好买第k个商品的概率。设概率为p/q，则输出y使得其满足：

题解：容易得出概率就为：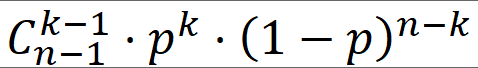

将公式两边同时乘q的逆元inv(q)，可得：

因为题目输入p给的是三位小数，所以直接将p乘以1000化为整数，最后答案再依次乘以1000的逆元就行。但是要注意的是，p化为整数时还要加个eps......然后可以开始补题了...

【有个快速求逆元的公式】：当p是质数时，a关于p的逆元为

【ACM中浮点数精度问题】：http://www.cnblogs.com/crazyacking/p/4668471.html

关于这题浮点数精度问题，我是这样想的，举个例子：

　　输入数p为0.001，但是你浮点数变量p存的值可能就变成了0.0010000001，或者变成了0.0009999999，所以这题乘以1000还要再加个eps，加0.2和加1e-10都没关系(看这题卡的精度吧)，但是因为是浮点数，其低位的不确定性使得你运算时必须加个eps...

题解参考：https://blog.csdn.net/black_miracle/article/details/70196798

代码如下：

 #include <bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 const ll mod = 1e9+;
 const double eps = 1e-;
 const int N = ;
 ll inv[N];
 int main() {
     int n, m, k, i, j;
     double p1;
     ll p, ans = ;

     inv[] = ;
     for(i = ; i < N; ++i)
         inv[i] = (mod - mod / i) * 1ll * inv[mod % i] % mod;

     scanf("%d%d%d%lf", &m, &n, &k, &p1);

     if(m < n || k > n) {puts(""); return ;}

     p = (ll)(p1 * 1000.0 + eps);
     //求组合数C(n-1, k-1)
     for(i = ; i <= k-; ++i) ans = (ans * (n-i)) % mod;
     for(i = ; i <= k-; ++i) ans = (ans * inv[i]) % mod;

     for(i = ; i <= k; ++i) ans = (ans * p) % mod;
     for(i = ; i <= n-k; ++i) ans = (ans * (-p)) % mod;
     //依次乘以1000关于mod的逆元
     for(i = ; i <= n; ++i) ans = (ans * inv[]) % mod;
     printf("%lld\n", ans);
     return ;
 }

31ms