Lotto HDU

链接

[http://acm.hdu.edu.cn/showproblem.php?pid=1342]

题意

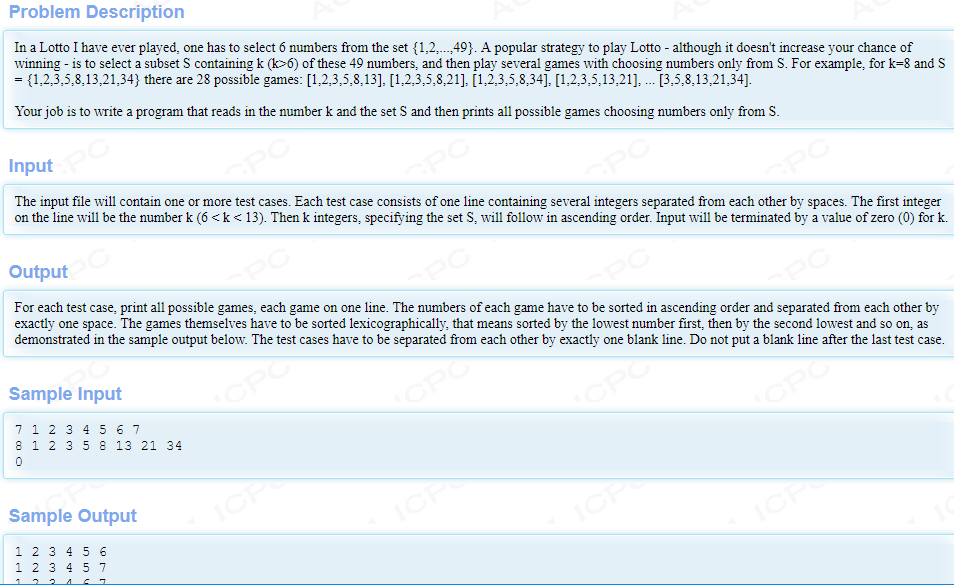
分析

DFS

代码

#include<cstdio>
#include<cstring>
int a[15],b[15],vis[15],k;
void dfs(int ans,int num)
{
    if(num==6)
    {
        for(int i=0;i<5;i++)
            printf("%d ",b[i]);
        printf("%d\n",b[5]);
        return;
    }
    for(int i=ans;i<k;i++)
    {
        if(!vis[i])
        {
            vis[i]=1;
            b[num]=a[i];
            dfs(i+1,num+1);
            vis[i]=0;
        }
    }
}

int main()
{
	freopen("in.txt","r")
    int flag=0;
    while(scanf("%d",&k)!=EOF&&k)
    {
        for(int i=0;i<k;i++)
            scanf("%d",&a[i]);
        if(flag) printf("\n");
        else flag=1;
        memset(vis,0,sizeof(vis));
        dfs(0,0);
    }
    return 0;
}