9.10NOIP模拟题

  9.10 NOIP模拟赛

题目名称	区间	种类	风见幽香
题目类型	传统	传统	传统
可执行文件名	section	kinds	yuuka
输入文件名	section.in	kinds.in	yuuka.in
输出文件名	section.out	kinds.out	yuuka.out
每个测试点时限	1.0秒	6.0秒	1.0秒
内存限制	256 MB	512 MB	128 MB
测试点数目	25	25	25
每个测试点分值	4	4	4

区间

Description

Hkd有一个长度为n的数列，元素互不相同。

Hkd一天走在路上捡到了一个数d。

Hkd很高兴，以为d恰好是她的数列中的数。

Hkd很天真的想知道她拥有的排列中，满足以下条件的区间的个数

1. 区间长度为奇数

2将区间元素排序后中间的数是d

Input

第一行输入两个整数n,d。

接下来一行n个整数为Hkd拥有的数列。

Output

输出一行表示答案

Example

Sample input 1

7 4

5 7 2 4 3 1 6

Sample output 1

4

/*
对于一个合法的区间，其比中位数p大的数的个数是等于比中位数p小的数的个数的。
那么记大于p的数为1，小于p的数为-1，等于p的数为0，对这个做一个前缀和，
并统计一下每个前缀和出现的次数，顺便维护一下中位数p的位置就好了。
*/
#include<iostream>
#include<cstdio>
#include<cstring>

#define N 200005
#define ll long long

using namespace std;
int a[N],b[N];
int n,m,x,ans,p;

const int BUF=;char Buf[BUF],*buf=Buf;
inline void read(int &now)
{
    for(now=;!isdigit (*buf);++buf);
    for(;isdigit(*buf);now=now*+*buf-'',++buf);
}

int main()
{
    freopen("section.in","r",stdin);
    freopen("section.out","w",stdout);
    fread(buf,,BUF,stdin);
    read(n);read(m);
    for(int i=;i<=n;i++)
    {
        read(x);
        if(x<m)b[i]=-;
        if(x==m) b[i]=,p=i;
        if(x>m) b[i]=;
        b[i]+=b[i-];
    }
    for(int i=;i<p;i++) a[b[i]+n]++;
    for(int i=p;i<=n;i++) ans+=a[b[i]+n];
    printf("%d\n",ans);
    return ;
}

种类

Description

Hkd的数列有n个数。

数列中的第i个数可以取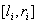中的随便一个值。

然后hkd有一个很神奇的法宝--S；

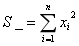
S=S_的种类数

Input

第一行一个数n。

接下来n行每行两个数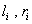

Output

输出一行一个数表示答案。

Example

Sample input 1

5

1 2

2 3

3 4

4 5

5 6

Sample output 1

26

Hint

 

/*
每个数的范围只有[1,100]同时最多只有100个数,所以S_的值最多有1000000个
然后的n^5方程很容易想到
表示前i个数能否得出和为j的数
然后我们惊奇的发现这个方程可以用bitset优化于是我们的时间复杂度变成了n^5/128。
*/
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<bitset>

#define N 1000001

using namespace std;

bitset<N>dp[];
int n,ai[],bi[];

inline int read()
{
    int x=,f=;char c=getchar();
    while(c>''||c<''){if(c=='-')f=-;c=getchar();}
    while(c>=''&&c<=''){x=x*+c-'';c=getchar();}
    return x*f;
}

int main()
{
    freopen("kinds.in","r",stdin);
    freopen("kinds.out","w",stdout);
    n=read();dp[]^=;
    for(int i=;i<=n;i++)
    {
        ai[i]=read(),bi[i]=read();
        for(int v=ai[i];v<=bi[i];v++) dp[i]|=dp[i-]<<(v*v);
    }
    cout<<dp[n].count();
    return ;
}

 

 

风见幽香

Description

幽香是幻想乡中的一个很萌的妹子，是一个1.3k岁的少女(雾)，某天，幽香正呆在自己的花田中赏花，突然一大波油库里从花田上空飞过，幽香感到一阵烦躁，她打算把它们打下来当花肥。

每个油库里都有两个属性，营养值和倍率。

整个天空可以抽象的看做是一个二维的平面直角坐标系，每个油库里可以看做是坐标系中的一个点。

幽香的攻击方式为用她的伞发出魔炮，具体的，魔炮可以看做是一个无限长的平行四边形，可以看做是两条倾斜角度为k的平行线夹得的区域，平行线间的距离是任意的，如下图所示。

。

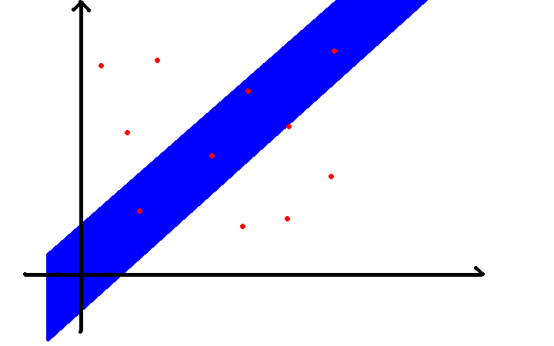
理论上每次在攻击范围之中的油库里都会被击落，变成花肥，在魔炮边界上的油库里也会被击落，也就是从坐标系中消失，每次攻击后可以得到的营养值为其中S表示此次攻击击落的油库里的集合，|S|表示集合的元素个数，即此次攻击击中的每一个油库里的营养值乘以此次所有被击落的油库里倍率的平均值。

幽香会使用若干次魔炮，直至击落所有的油库里，且任意两次攻击范围不会重叠，最后得到的营养值为每次攻击得到的营养值之和。现在幽香想要知道在击落所有的油库里后，她总共能获得多少营养值。若是你不会的话....哼哼，她可是会把你做成花肥了啊。

Input

第1行，1个整数N，表示油库里个数。

第2...N+1行，每行四个整数x,y,v,c，表示油库里的坐标(x,y)，以及v和c。

第N+2行：1个整数k，表示倾斜角角度，0°到180°。

Output

输出一行，为最大营养值(保留3位小数)(你的答案必须与标准输出完全一样)。

Example

Sample input 1

3

1 3 3 1

2 1 2 2

3 4 2 1

45

Sample output 1

9.333

/*
考虑以下事实，攻击的范围是两条固定斜率的直线夹得的区域，
那么，直角坐标系中的每个点就有都有了一个固定的斜率，
所以每个点所在的直线也就能随之确定下来，那么我们按照每个点所在直线的纵截距排序，
那么问题就转变为了区间里的问题。
所以考虑区间dp，设dp[i]为第i条直线之前的所有价值。
需要前缀和优化
*/
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>

#define N 2017
#define phi 3.1415926

using namespace std;
double f[N],sc[N],sv[N];
int n,s[N];
double ans,k;
struct node
{
    double x,y;
    double v,c,b;
}a[N];

inline bool cmp(node a,node b){return a.b<b.b;}
inline double max(double a,double b){return a>b?a:b;}

int main()
{
    freopen("yuuka.in","r",stdin);
    freopen("yuuka.out","w",stdout);
    scanf("%d",&n);
    for(int i=;i<=n;i++)
      scanf("%lf%lf%lf%lf",&a[i].x,&a[i].y,&a[i].v,&a[i].c);
    if(k==||k==) k=;
    scanf("%lf",&k);k=tan(k/*phi);

    for(int i=;i<=n;i++)
      a[i].b=a[i].y-a[i].x*k;
    sort(a+,a+n+,cmp);
    int pos=;s[]=pos;sc[]=a[].c;sv[]=a[].v;
    for(int i=;i<=n;i++)
    {
        if(a[i].b!=a[i-].b)
        pos++,s[i]=s[i-],sc[i]=sc[i-],sv[i]=sv[i-];
        ++s[i];sc[i]+=a[i].c;sv[i]+=a[i].v;
    }

    for(int i=;i<=pos;i++)
    {
        f[i]=sv[i]*sc[i]/s[i];
        for(int j=;j<i;j++)
          f[i]=max(f[i],f[j]+(sv[i]-sv[j])*(sc[i]-sc[j])/(s[i]-s[j]));
    }
    printf("%.3lf",f[n]);
    fclose(stdin);fclose(stdout);
    return ;
}