HDU 6073 Matching In Multiplication dfs遍历环 + 拓扑

Matching In Multiplication

Problem Description
In the mathematical discipline of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V (that is, U and V are each independent sets) such that every edge connects a vertex in U to one in V. Vertex sets U and V are usually called the parts of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles. A matching in a graph is a set of edges without common vertices. A perfect matching is a matching that each vertice is covered by an edge in the set.

　　　　　　　　　　　　　　　　　　　　　　　

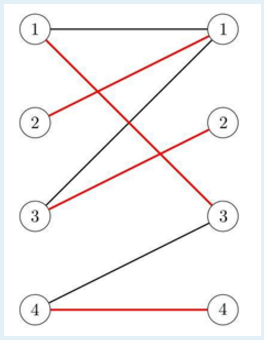
Little Q misunderstands the definition of bipartite graph, he thinks the size of U is equal to the size of V, and for each vertex p in U, there are exactly two edges from p. Based on such weighted graph, he defines the weight of a perfect matching as the product of all the edges' weight, and the weight of a graph is the sum of all the perfect matchings' weight.

Please write a program to compute the weight of a weighted ''bipartite graph'' made by Little Q.

Input
The first line of the input contains an integer T(1≤T≤15), denoting the number of test cases.

In each test case, there is an integer n(1≤n≤300000) in the first line, denoting the size of U. The vertex in U and V are labeled by 1,2,...,n.

For the next n lines, each line contains 4 integers vi,1,wi,1,vi,2,wi,2(1≤vi,j≤n,1≤wi,j≤109), denoting there is an edge between Ui and Vvi,1, weighted wi,1, and there is another edge between Ui and Vvi,2, weighted wi,2.

It is guaranteed that each graph has at least one perfect matchings, and there are at most one edge between every pair of vertex.

Output
For each test case, print a single line containing an integer, denoting the weight of the given graph. Since the answer may be very large, please print the answer modulo 998244353.

Sample Input
1
2
2 1 1 4
1 4 2 3

Sample Output
16

题意：

　　给你一个图，n点 2*n边，有边权。

　　左边的1~n个点出度都为2，且都连向右边的点，两点之间，没有重边，求出每种完美匹配下各边乘积的总和

题解：

　　不好好写就会wa死你哦，咕咕咕

　　首先如果一个点的度数为11，那么它的匹配方案是固定的，继而我们可以去掉这一对点。通过拓扑我们可以不断去掉所有度数为11的点。

　　那么剩下的图中左右各有mm个点，每个点度数都不小于22，且左边每个点度数都是22，而右侧总度数是2m2m，

　　因此右侧只能是每个点度数都是22。这说明这个图每个连通块是个环，在环上间隔着取即可，一共两种方案。

　　时间复杂度O(n)O(n)

#include<bits/stdc++.h>
using namespace std;
#pragma comment(linker, "/STACK:102400000,102400000")
#define ls i<<1
#define rs ls | 1
#define mid ((ll+rr)>>1)
#define pii pair<int,int>
#define MP make_pair
typedef long long LL;
const long long INF = 1e18+1LL;
const double pi = acos(-1.0);
const int N = 1e6+, M = 1e3+,inf = 2e9;

const LL mod = 998244353LL;

queue<pii > q;
int vis[N],done[N],d[N],n,T,zhong;
LL ans1,ans2;
vector<pii > G[N];
void init() {
    for(int i = ; i <= *n; ++i)
        G[i].clear(),vis[i] = ,done[i] = ,d[i] = ;
}
void dfs(int u,int f,int p) {
    vis[u] = ;
    int flag = ;
    for(int i = ; i < G[u].size(); ++i) {
        int to = G[u][i].first;
        if(vis[to]) continue;
        flag = ;
        if(!p) ans1 = 1LL * ans1 * G[u][i].second % mod;
        else ans2 = 1LL * ans2 * G[u][i].second % mod;
        dfs(to,u, - p);
    }
    if(flag) {
        for(int i = ; i < G[u].size(); ++i) {
            int to = G[u][i].first;
            if(to != zhong) continue;
            if(!p) ans1 = 1LL * ans1 * G[u][i].second % mod;
            else ans2 = 1LL * ans2 * G[u][i].second % mod;
        }
    }
}
void make_faiil(int u,int f,int p) {
    done[u] = ;
    vis[u] =;
    for(int i = ; i < G[u].size(); ++i) {
        int to = G[u][i].first;
        if(to == f || done[to]) continue;
        make_faiil(to,u, - p);
    }
}
int main() {
    scanf("%d",&T);
    while(T--) {
        scanf("%d",&n);
        init();
        for(int i = ; i <= n; ++i) {
            int x,y;
            scanf("%d%d",&x,&y);
            d[i] += ;
            d[x + n] += ;
            G[i].push_back(MP(x + n,y));
            G[x + n].push_back(MP(i,y));

            scanf("%d%d",&x,&y);
            d[i] += ;
            d[x + n] += ;
            G[i].push_back(MP(x + n,y));
            G[x + n].push_back(MP(i,y));
        }
        int ok = ;
        while(!q.empty()) q.pop();
        for(int i = n+; i <= *n; ++i) {
            if(d[i] == ) {
                q.push(MP(i,));
                vis[i] = ;
            }
        }
        LL ans = 1LL;
        while(!q.empty()) {
            pii k = q.front();
            q.pop();
            for(int i = ; i < G[k.first].size(); ++i) {
                int to = G[k.first][i].first;
                if(vis[to]) continue;
                d[to] -= ;
                if(d[to] == ) {
                    if(!k.second)ans = ans * G[k.first][i].second % mod;
                    q.push(MP(to,!k.second));
                    vis[to] = ;
                }
            }
        }
        //cout<<ans<<endl;
        LL tmp1 = ans,tmp2 = ;
        for(int i = ; i <= *n; ++i) {
            if(!vis[i]){
              //  cout<<"huasndina " << i<<endl;
                ans1 = 1LL,ans2 = 1LL;
                zhong = i;
                dfs(i,-,);
                LL tmptmp = (ans1 + ans2) % mod;
                ans = ans * tmptmp % mod;
            }
        }
        printf("%lld\n",(ans)%mod);
    }
    return ;
}

/*
10
5
1 1 2 3
1 2 3 4
3 5 4 7
3 6 4 8
4 9 5 10
4920
*/