AVL树（平衡二叉树）

定义及性质

　　AVL树：AVL树是一颗自平衡的二叉搜索树.

　　AVL树具有以下性质：

　　　　根的左右子树的高度只差的绝对值不能超过1

　　　　根的左右子树都是 平衡二叉树（AVL树）

百度百科：

　　平衡二叉搜索树（Self-balancing binary search tree）又被称为AVL树（有别于AVL算法）

　　　　且具有以下性质：它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

　　　　平衡二叉树的常用实现方法有红黑树、AVL、替罪羊树、Treap、伸展树等。

　　 　　　　最小二叉平衡树的节点总数的公式如下 F(n)=F(n-1)+F(n-2)+1 这个类似于一个递归的数列，

　　　　 　　可以参考Fibonacci(斐波那契)数列，1是根节点，F(n-1)是左子树的节点数量，F(n-2)是右子树的节点数量。

AVL树--插入操作

AVL插入--旋转

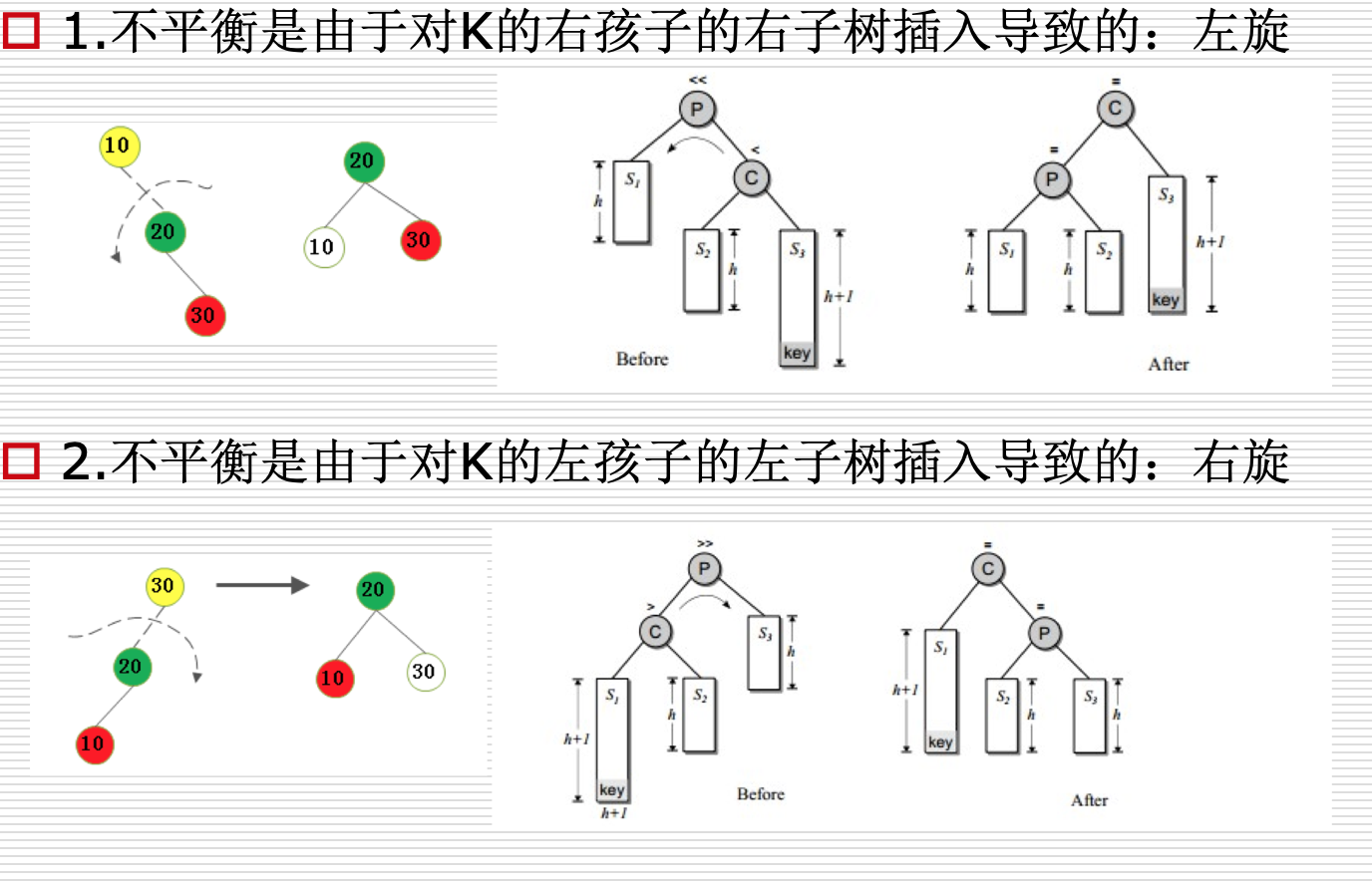
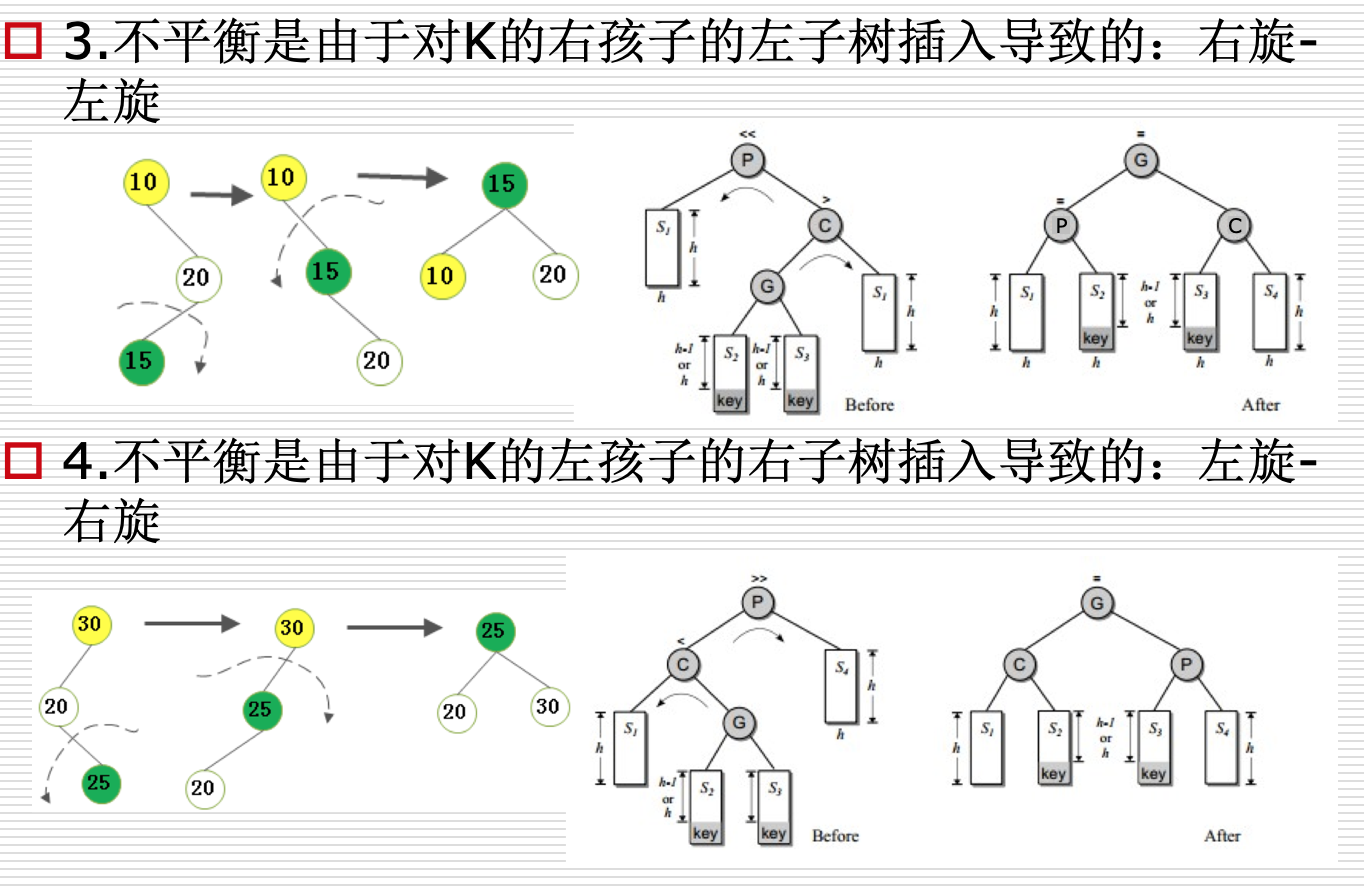
代码实现

from bst import BST, BiTreeNode

class AVLNode(BiTreeNode):
    def __init__(self, data):
        BiTreeNode.__init__(self, data)
        self.bf = 0

class AVLTree(BST):
    def __init__(self, li=None):
        BST.__init__(self, li)

    def rotate_left(self, p, c):
        s2 = c.lchild
        p.rchild = s2
        if s2:
            s2.parent = p

        c.lchild = p
        p.parent = c

        # 更新bf
        if c.bf == 0:
            p.bf = 1
            c.bf = -1
        else:
            p.bf = 0
            c.bf = 0
        return c

    def rotate_right(self, p, c):
        s2 = c.rchild
        p.lchild = s2
        if s2:
            s2.parent = p

        c.rchild = p
        p.parent = c

        # update bf
        if c.bf == 0:
            p.bf = -1
            c.bf = 1
        else:
            p.bf = 0
            c.bf = 0
        return c

    def rotate_right_left(self, p, c):
        g = c.lchild

        s3 = g.rchild
        c.lchild = s3
        if s3:
            s3.parent = c
        g.rchild = c
        c.parent = g

        s2 = g.lchild
        p.rchild = s2
        if s2:
            s2.parent = p
        g.lchild = p
        p.parent = g

        # 更新 bf
        if g.bf > 0:  # g.bf == 1
            p.bf = -1
            c.bf = 0
        elif g.bf == 0:
            p.bf = 0
            c.bf = 0
        else: # g.bf == -1
            p.bf = 0
            c.bf = 1

        g.bf = 0
        return g

    def rotate_left_right(self, p, c):
        g = c.rchild

        s3 = g.lchild
        c.rchild = s3
        if s3:
            s3.parent = c
        g.lchild = c
        c.parent = g

        s2 = g.rchild
        p.lchild = s2
        if s2:
            s2.parent = p
        g.rchild = p
        p.parent = g

        # 更新 bf
        if g.bf < 0:  # g.bf == 1
            p.bf = 1
            c.bf = 0
        elif g.bf == 0:
            p.bf = 0
            c.bf = 0
        else:  # g.bf == -1
            p.bf = 0
            c.bf = -1

        g.bf = 0
        return g

    def insert_no_rec(self, val):
        p = self.root
        if not p:
            self.root = AVLNode(val)
            return
        while True:
            if val < p.data:
                if p.lchild:
                    p = p.lchild
                else:
                    p.lchild = AVLNode(val)
                    p.lchild.parent = p
                    node = p.lchild
                    break
            elif val > p.data:
                if p.rchild:
                    p = p.rchild
                else:
                    p.rchild = AVLNode(val)
                    p.rchild.parent = p
                    node = p.rchild
                    break
            else:
                return

        # 更新bf
        while node.parent:
            if node.parent.lchild == node:  # 左孩子
                if node.parent.bf < 0: # node.parent.bf=-2 左边深
                    g = node.parent.parent
                    if node.bf > 0:
                        n = self.rotate_left_right(node.parent, node)
                    else:
                        n = self.rotate_right(node.parent, node)
                elif node.parent.bf > 0:
                    node.parent.bf = 0
                    break
                else:
                    node.parent.bf = -1
                    node = node.parent
                    continue

            else:  # 右孩子
                if node.parent.bf > 0: # node.parent.bf=2 右边深
                    g = node.parent.parent
                    if node.bf < 0:
                        n = self.rotate_right_left(node.parent, node)
                    else:
                        n = self.rotate_left(node.parent, node)
                elif node.parent.bf < 0:
                        node.parent.bf = 0
                        break
                else:
                    node.parent.bf = 1
                    node = node.parent
                    continue

            # 旋转结束后
            # 连接旋转后的子树的根和原来的树

            n.parent = g
            if g:
                if node.parent == g.lchild:
                    g.lchild = n
                else:
                    g.rchild = n
                break
            else:
                self.root = n
                break

tree = AVLTree([7,3,5,4,2,8,6,9,1])
tree.pre_order(tree.root)
print("")
tree.in_order(tree.root)