RMQ（Range Minimum Query）问题（转）

问题描述

RMQ问题是求给定区间中的最值问题。对于长度为n的数列A，回答若干查询RMQ(A, i, j)。返回数组A中下标在[i，j]里的最小值的下标。

比如数列 5,8,1,3,6,4,9,5,7      那么RMQ(2,4) = 3， RMQ(6,9) = 6.

 

解决问题

最简单的解法时间复杂度是O（n），就是对于每一个查询遍历一遍数组。但是当n非常大的时候，并且查询次数非常多的时候，这个解决方案就不是那么高效了。

使用线段树（以后会讲）可以将时间复杂度优化到O（logn），通过在线段树中保存线段的最值。

不过本文将介绍一个解决RMQ最强大的算法，Sparse-Table算法。

Sparse-Table算法是一个在线算法，所 谓在线算法，是指用户每输入一个查询便马上处理一个查询。该算法一般用较长的时间做预处理，待信息充足以后便可以用较少的时间回答每个查询。 ST（Sparse Table）算法是一个非常有名的在线处理RMQ问题的算法，它可以在O(nlogn)时间内进行预处理，然后在O(1)时间内回答每个查询。

首 先是预处理，用动态规划（DP）解决。设A[i]是要求区间最值的数列，F[i, j]表示从第i个数起连续2^j个数中的最大值。例如数列3 2 4 5 6 8 1 2 9 7，F[1，0]表示第1个数起，长度为2^0=1的最大值，其实就是3这个数。 F[1，2]=5，F[1，3]=8，F[2，0]=2，F[2，1]=4……从这里可以看出F[i,0]其实就等于A[i]。这样，DP的状态、初值都 已经有了，剩下的就是状态转移方程。我们把F[i，j]平均分成两段（因为f[i，j]一定是偶数个数字），从i到i+2^(j-1)-1为一 段，i+2^(j-1)到i+2^j-1为一段(长度都为2^（j-1）)。用上例说明，当i=1，j=3时就是3,2,4,5 和 6,8,1,2这两段。F[i，j]就是这两段的最大值中的最大值。于是我们得到了动态规划方程F[i, j]=max（F[i，j-1], F[i + 2^(j-1)，j-1]）。

然 后是查询。取k=[log2(j-i+1)]，则有：RMQ(A, i, j)=max{F[i,k],F[j-2^k+1,k]}。 举例说明，要求区间[2，8]的最大值，总共2到8是7个元素，所以k=2，那么就要把它分成[2,5]和[5,8]两个区间，因为这两个区间的最大值我 们可以直接由f[2，2]和f[5，2]得到。

具体如下图所示：

 

算法伪代码

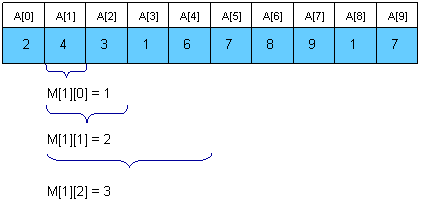
//初始化

 

INIT_RMQ

 

//max[i][j]中存的是重i开始的2^j个数据中的最大值，最小值类似，num中存有数组的值

 

for i : 1 to n

 

  max[i][0] = num[i]

 

for j : 1 to log(n)

 

  for i : 1 to (n-2^j+1)

 

     max[i][j] = MAX（max[i][j-1], max[i+2^(j-1)][j-1]）

 

//查询

 

RMQ(i, j)

 

k = log(j-i+1)

 

return MAX(max[i][k], max[j-2^k+1][k])