第四章 模块化React和Redux应用

第四章 模块化React和Redux应用

4.1 模块化应用要点

构建一个应用的基础：

　　代码文件的组织结构；

　　确定模块的边界；

　　Store的状态树设计。

4.2 代码文件的组织方式

4.2.1 按角色组织

　　在MVC中，应用代码分为Controller、Model、View，分别代表三种模块角色。分别放到controllers、models、views目录下。

　　在Redux应用的构建中，把目录换成了：

　　reducer：目录中包含所有的Redux的reducer；

　　actions：包含所有action构造函数；

　　components：包含所有的傻瓜组件；

　　containers：包含所有的容器组件。

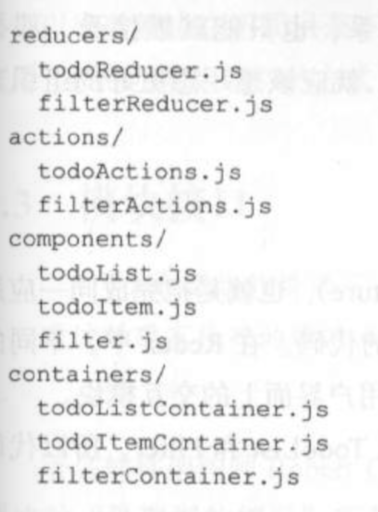
4.2.2 按功能组织

　　Redux应用适合于“按功能组织”，也就是把完成同一应用功能的代码放在一个目录下，一个应用功能包含多个角色的代码。应用功能对应的就是用户界面上的交互模块。

4.3 模块接口

低耦合性：不同功能模块之间的依赖关系应该简单而助清晰；

高内聚性：一个模块应该把自己的功能封装的很好，让外界不要太依赖于自己内部的结构，这样不会因为内部的变化而影响外部模块的功能。

在Redux应用中，整体由模块构成，但是模块不再是React组件，而是由React组件加上相关的reducer和actions构成的一个小整体。

导出模块的两种方式

import * as actions from ’. /actions;
import reducer from ’. /reducer;
import view from ’./views/container

export {actions, reducer, view)

导入

import {actions , reducer, view as TodoList) from ’.. / todoList

导出

 import* as actions from '. /actions
import reducer from ’. /reducer
import view from ’./views/conta工ner
export default {act工ons, reducer, view}

导入

import TodoListComponent from ’. /actions
const reducer = TodoListComponent .reducer;
const actions = TodoListComponent .actions;
const TodoList = TodlistComponent.view

4.4 状态树的设计

所有的状态都存在Store上，Store的状态树设计，直接决定了要写哪些reducer，还有action怎么写，是程序逻辑的源头。

状态树设计要遵循以下几个原则：

　　一个模块控制一个状态节点；

　　避免冗余数据；

　　树形结构扁平。

4.4.1 一个状态节点只属于一个模块

　　在Redux应用中，Store上的每个state都只能通过reducer来更改，而我们每个模块都有机会导出一个自己的reducer，这个导出的reducer只能最多更改Redux的状态树上一个节点下的数据，不同模块下的reducer不能互相修改