poj 1330 Nearest Common Ancestors LCA

题目链接：http://poj.org/problem?id=1330

A rooted tree is a well-known data structure in computer science and engineering. An example is shown below:

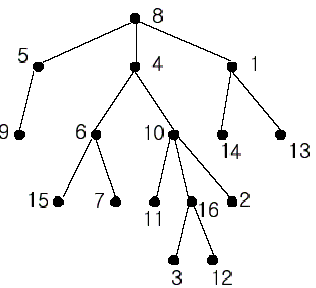
In the figure, each node is labeled with an integer from {1, 2,...,16}. Node 8 is the root of the tree. Node x is an ancestor of node y if node x is in the path between the root and node y. For example, node 4 is an ancestor of node 16. Node 10 is also an ancestor of node 16. As a matter of fact, nodes 8, 4, 10, and 16 are the ancestors of node 16. Remember that a node is an ancestor of itself. Nodes 8, 4, 6, and 7 are the ancestors of node 7. A node x is called a common ancestor of two different nodes y and z if node x is an ancestor of node y and an ancestor of node z. Thus, nodes 8 and 4 are the common ancestors of nodes 16 and 7. A node x is called the nearest common ancestor of nodes y and z if x is a common ancestor of y and z and nearest to y and z among their common ancestors. Hence, the nearest common ancestor of nodes 16 and 7 is node 4. Node 4 is nearer to nodes 16 and 7 than node 8 is.

For other examples, the nearest common ancestor of nodes 2 and 3 is node 10, the nearest common ancestor of nodes 6 and 13 is node 8, and the nearest common ancestor of nodes 4 and 12 is node 4. In the last example, if y is an ancestor of z, then the nearest common ancestor of y and z is y.

Write a program that finds the nearest common ancestor of two distinct nodes in a tree. 

题意描述：在一个DAG中，定义节点u是节点v的祖先：节点u是树根到节点v的路径上的一个节点。 给出一些节点之间的关系，求出两个节点的最近公共祖先。

算法分析：最近公共祖先（LCA）的入门题。

最近公共祖先算法的大致思路：

1：求出每个节点的2^k（0<=k<max_log_n）的祖先节点。节点u的2^0（第一代）祖先节点就是u的父亲节点，那么我们可以得到u的第一代、第二代、第四代、第八代...祖先节点。

2：把节点u和v深度大的节点根据1中的算法思想移到和深度小的节点同一深度（树根深度为0，树根的儿子节点深度为1），然后再一起往上移，即可求出LCA。

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<cstdlib>
 #include<cmath>
 #include<algorithm>
 #include<vector>
 #define inf 0x7fffffff
 using namespace std;
 const int maxn=+;
 const int max_log_maxn=;

 int n,A,B,root;
 vector<int> G[maxn];
 int father[max_log_maxn][maxn],d[maxn];

 void dfs(int u,int p,int depth)
 {
     father[][u]=p;
     d[u]=depth;
     int num=G[u].size();
     for (int i= ;i<num ;i++)
     {
         int v=G[u][i];
         if (v != father[][u]) dfs(v,u,depth+);
     }
 }

 void init()
 {
     dfs(root,-,);
     for (int k= ;k+<max_log_maxn ;k++)
     {
         for (int i= ;i<=n ;i++)
         {
             if (father[k][i]<) father[k+][i]=-;
             else father[k+][i]=father[k][father[k][i] ];
         }
     }
 }

 int LCA()
 {
     if (d[A]<d[B]) swap(A,B);
     for (int k= ;k<max_log_maxn ;k++)
     {
         if ((d[A]-d[B])>>k & )
         {
             A=father[k][A];
         }
     }
     if (A==B) return A;
     for (int k=max_log_maxn- ;k>= ;k--)
     {
         if (father[k][A] != father[k][B])
         {
             A=father[k][A];
             B=father[k][B];
         }
     }
     return father[][A];
 }

 int main()
 {
     int t;
     scanf("%d",&t);
     while (t--)
     {
         scanf("%d",&n);
         for (int i= ;i<=n ;i++) G[i].clear();
         for (int i= ;i<max_log_maxn ;i++)
         {
             for (int j= ;j<maxn ;j++)
                 father[i][j]=-;
         }
         int a,b;
         int vis[maxn];
         memset(vis,,sizeof(vis));
         for (int i= ;i<n- ;i++)
         {
             scanf("%d%d",&a,&b);
             G[a].push_back(b);
             vis[b]=;
         }
         scanf("%d%d",&A,&B);
         for (int i= ;i<=n ;i++) if (!vis[i]) {root=i;break; }
         init();
         printf("%d\n",LCA());
     }
     return ;
 }