poj----（1470）Closest Common Ancestors（LCA）

Closest Common Ancestors

Time Limit: 2000MS		Memory Limit: 10000K
Total Submissions: 15446		Accepted: 4944

Description

Write a program that takes as input a rooted tree and a list of pairs of vertices. For each pair (u,v) the program determines the closest common ancestor of u and v in the tree. The closest common ancestor of two nodes u and v is the node w that is an ancestor of both u and v and has the greatest depth in the tree. A node can be its own ancestor (for example in Figure 1 the ancestors of node 2 are 2 and 5)

Input

The data set, which is read from a the std input, starts with the tree description, in the form:

nr_of_vertices

vertex:(nr_of_successors) successor1 successor2 ... successorn

...

where vertices are represented as integers from 1 to n ( n <= 900
). The tree description is followed by a list of pairs of vertices, in
the form:

nr_of_pairs

(u v) (x y) ...

The input file contents several data sets (at least one).

Note that white-spaces (tabs, spaces and line breaks) can be used freely in the input.

Output

For
each common ancestor the program prints the ancestor and the number of
pair for which it is an ancestor. The results are printed on the
standard output on separate lines, in to the ascending order of the
vertices, in the format: ancestor:times

For example, for the following tree:

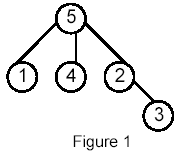
Sample Input

5
5:(3) 1 4 2
1:(0)
4:(0)
2:(1) 3
3:(0)
6
(1 5) (1 4) (4 2)
      (2 3)
(1 3) (4 3)

Sample Output

2:1
5:5

Hint

Huge input, scanf is recommended.

Source

Southeastern Europe 2000

 

给你一棵树，要你找出一些节点的最近公共祖先

 

代码：

 /*poj 1470*/
 #include<iostream>
 #include<vector>
 #include<cstdio>
 #include<cstring>
 #include<cstdlib>
 using namespace std;
 const int maxn=;
 vector<int> tree[maxn],qus[maxn];
 int rank[maxn],father[maxn];
 bool vis[maxn];
 int rudu[maxn];
 int lroot[maxn];
 int ans[maxn];

 void init(int n){
      memset(vis,,sizeof(char)*(n+));
      memset(rudu,,sizeof(int)*(n+));
      memset(lroot,,sizeof(int)*(n+));
      memset(ans,,sizeof(int)*(n+));
     for(int i=;i<=n;i++){
         father[i]=i;
         rank[i]=;
         tree[i].clear();
         qus[i].clear();
     }
 }

 int find(int a){
    while(a!=father[a])
          a=father[a];
     return a;
 }

 void Union(int a,int b)
 {
     int x=find(a);
     int y=find(b);
     if(x==y) return ;
     if(rank[x]<rank[y]){
       rank[y]+=rank[x];
       father[x]=y;
     }
     else {
      rank[x]+=rank[y];
      father[y]=x;
     }
 }

 void LCA(int u)
 {
   lroot[u]=u;
   //vis[u]=1; 不能放在这里
   int len=tree[u].size();
   for(int i=;i<len;i++){
       LCA(tree[u][i]);
       Union(u,tree[u][i]);
       lroot[find(u)]=u;
   }
   vis[u]=;
   int ss=qus[u].size();
   for(int i=;i<ss;i++){
         if(vis[qus[u][i]]){
             ans[lroot[find(qus[u][i])]]++;
             //return ;
         }
   }
 }

 int main()
 {
     int n,m,t,u1,u2;
     freopen("test.in","r",stdin);
     while(scanf("%d",&n)!=EOF){
           init(n);
       for(int i=;i<n;i++){
             getchar();
         scanf("%d:(%d))",&u1,&m);
          for(int j=;j<m;j++){
              scanf("%d",&u2);
              tree[u1].push_back(u2);
              rudu[u2]++;
          }
         }
       scanf("%d",&t);
       for(int i=;i<t;i++)
       {
           scanf("%*1s%d%d%*1s",&u1,&u2);
           qus[u1].push_back(u2);
           qus[u2].push_back(u1);
       }
       for(int i=;i<=n;i++)
       {
           if(rudu[i]==)
         {
             LCA(i);
             break;
         }
       }
       for(int i=;i<=n;i++){
           if(!=ans[i])
             printf("%d:%d\n",i,ans[i]);
       }
     }
 return ;
 }