希尔排序的理解和实现(Java)

希尔排序原理

希尔排序（shell sort）这个排序方法又称为缩小增量排序，是1959年D·L·Shell提出来的。

该方法的基本思想是：设待排序元素序列有n个元素，首先取一个整数increment（小于n）作为间隔将全部元素分为increment个子序列，所有距离为increment的元素放在同一个子序列中，在每一个子序列中分别实行直接插入排序。然后缩小间隔increment，重复上述子序列划分和排序工作。直到最后取increment=1，将所有元素放在同一个子序列中排序为止。

由于开始时，increment的取值较大，每个子序列中的元素较少，排序速度较快，到排序后期increment取值逐渐变小，子序列中元素个数逐渐增多，但由于前面工作的基础，大多数元素已经基本有序，所以排序速度仍然很快。

希尔排序流程

1、给出一个待排序的数据列：

2、第一趟取increment的方法是：n/3向下取整+1=3（关于increment的取法之后会有介绍）。将整个数据列划分为间隔为3的3个子序列，然后对每一个子序列执行直接插入排序，相当于对整个序列执行了部分排序调整。图解如下：

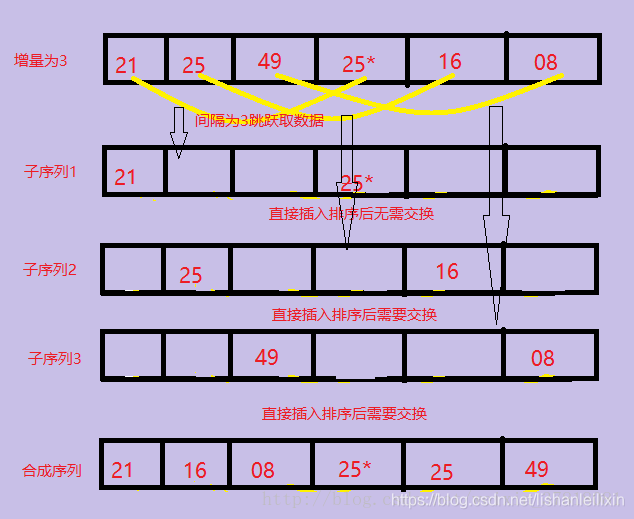3、第二趟将间隔increment= increment/3向下取整+1=2，将整个元素序列划分为2个间隔为2的子序列，分别进行排序。图解如下：



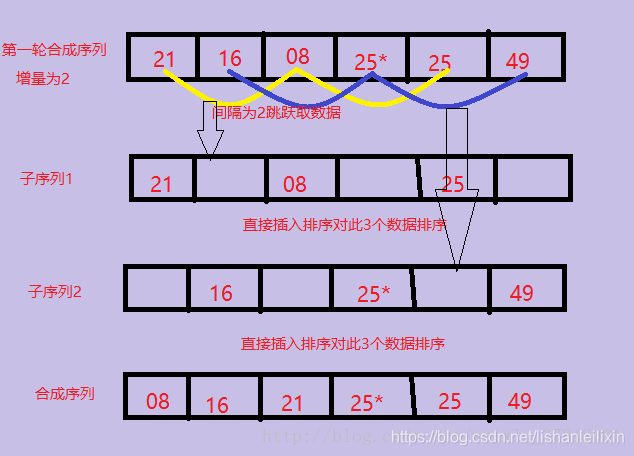
4、第3趟把间隔缩小为increment= increment/3向下取整+1=1，当增量为1的时候，实际上就是把整个数列作为一个子序列进行插入排序，图解如下：



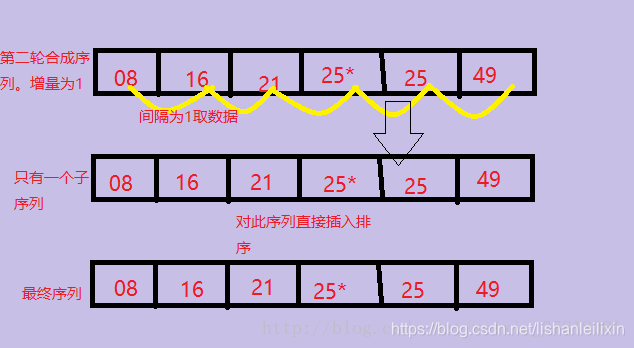
5、直到increment=1时，就是对整个数列做最后一次调整，因为前面的序列调整已经使得整个序列部分有序，所以最后一次调整也变得十分轻松，这也是希尔排序性能优越的体现。

希尔排序实现代码：

public class ShellSort {

	public void shellSort(int[] elem) {
		int i, j;
		int increment = elem.length;

		do {
			increment = increment / 3 + 1;
			for (i = increment + 1; i < elem.length; i++) {
				if(elem[i] < elem[i - increment]) {
					elem[0] = elem[i];
					for (j = i - increment; j > 0 && elem[0] < elem[j]; j -= increment) {
						elem[j + increment] = elem[j];
					}
					elem[j + increment] = elem[0];
				}
			}
		} while(increment > 1);
	}

	public static void main(String[] args) {
		int[] elem = {0, 9, 1, 5, 8, 3, 7, 4, 6, 2};
		ShellSort s = new ShellSort();
		s.shellSort(elem);
		for (int i = 1; i < elem.length; i++) {
			System.out.print(elem[i] + ", ");
		}

	}
}

增量increment的取法

增量increment的取法有各种方案。最初shell提出取increment=n/2向下取整，increment=increment/2向下取整，直到increment=1。但由于直到最后一步，在奇数位置的元素才会与偶数位置的元素进行比较，这样使用这个序列的效率会很低。后来Knuth提出取increment=n/3向下取整+1.还有人提出都取奇数为好，也有人提出increment互质为好。应用不同的序列会使希尔排序算法的性能有很大的差异。

希尔排序复杂度分析

对于希尔排序其增量increment的选择非常关键，最燃至今其怎样选择还是一个数学难题，但是通过大量研究表明，当增量序列为dlta[k]=2t−k+12^{t-k+1}2t−k+1-1（0≤k≤t≤log2log_2log2​(n+1)）时，可以获得不错的效率，其时间复杂度为O(n3/2n^{3/2}n3/2)，要好于直接排序的O(n2n^2n2)，需要注意的是增量序列的最后一个增量值必须等于1才行。另外由于记录是跳跃性的移动，希尔排序并不是一种稳定的排序算法。

本文参考：https://blog.csdn.net/weixin_37818081/article/details/79202115