AtCoder | ARC103 | 瞎讲报告

目录

• ARC 103
  • A.////
  • B.Robot Arms
  • C.Tr/ee
  • D.Distance Sums

ARC 103

窝是传送门QwQ

A.////

题意 :

给你\(n\)(\(n\)为偶数)个数 一次操作你可以修改任意一个数

问最少修改几次使得其满足以下条件

• \(a_i=a_{i+2}\)
• \(a_1!=a_2\)

数据约束：

\(2 \leq n \leq 10^5\) , \(1 \leq a_i \leq 10^5\)

题解：

对于下标为奇数的记下每个数出现的个数 在满足和偶数不重复的情况下 贪心肯定是尽量选大的嘛

偶数同理啊

Code

代码写丑了

#include<bits/stdc++.h>
#define fr(i,x,y) for(int i=x;i<=y;++i)
#define rf(i,x,y) for(int i=x;i>=y;--i)
#define LL long long
using namespace std;
const int N=1e5+10,M=1e5;
int a[N];
struct data{
    int id,w;
}b[N],zz[5];
int vis[N];

bool cmp(data x,data y){
    return x.w>y.w;
}

int main(){
    int n;scanf("%d",&n);
    int ans=0,res=0;
    fr(i,1,n) scanf("%d",&a[i]);
    for(int i=1;i<=n;i+=2) vis[a[i]]++;
    fr(i,1,M) b[++res].id=i,b[res].w=vis[i];
    sort(b+1,b+1+res,cmp);
    zz[1]=b[1],zz[2]=b[2];
    memset(vis,0,sizeof vis);
    for(int i=2;i<=n;i+=2) vis[a[i]]++;
    res=0;
    fr(i,1,M) b[++res].id=i,b[res].w=vis[i];
    sort(b+1,b+1+res,cmp);
    zz[3]=b[1],zz[4]=b[2];
    int maxn=0;
    fr(i,1,2) fr(j,3,4){
        if(zz[i].id!=zz[j].id) maxn=max(maxn,zz[i].w+zz[j].w);
    }
    cout<<n-maxn<<endl;
    return 0;
}

---

B.Robot Arms

题意：

给你\(n\)个平面上的点 一个机器人从\((0,0)\)出发 执行\(m\)次操作 每次操作可以往上下左右走\(d_i\)长度

\(d_i,m\)是自己构造的 使得对于给出的点 每次机器人从\((0,0)\)出发 走\(m\)步上下左右构造

数据约束：

\(m \leq 40 ,\) \(1 \leq n \leq 1000\) ,\(-10^9 \leq x,y \leq 10^9\)

题解：

二进制拆分

Code

#include<bits/stdc++.h>
#define fr(i,x,y) for(int i=x;i<=y;++i)
#define rf(i,x,y) for(int i=x;i>=y;--i)
#define LL long long
using namespace std;
const int N=1010;
struct data{
    LL x,y;
}a[N];
int dx[4]={1,0,-1,0};
int dy[4]={0,-1,0,1};
char ch[4]={'R','D','L','U'};
vector<LL>v;

int main(){
    int n;scanf("%d",&n);
    fr(i,1,n) scanf("%lld%lld",&a[i].x,&a[i].y);
    int flg=0;
    fr(i,1,n){
        if(i==1) flg=(a[i].x+a[i].y)&1;
        else if(flg!=((a[i].x+a[i].y)&1)) return printf("-1\n"),0;
    }
    rf(i,30,0) v.push_back(1LL<<i);
    if(!flg) v.push_back(1);
    int len=v.size();
    printf("%d\n",len);
    fr(i,0,len-1) printf("%lld ",v[i]);
    puts("");
    fr(i,1,n){
        LL xx=a[i].x,yy=a[i].y;
        fr(j,0,len-1){
            LL minn=1e18,res=-1;
            fr(o,0,3){
                LL nx=xx-v[j]*dx[o],ny=yy-v[j]*dy[o];
                if(minn>abs(nx)+abs(ny)) minn=abs(nx)+abs(ny),res=o;
            }
            xx-=v[j]*dx[res],yy-=v[j]*dy[res];
            printf("%c",ch[res]);
        }
        puts("");
    }
    return 0;
}

---

C.Tr/ee

题意：

给你一个序列\(s[]\) 构造出一棵\(n\)个节点的树

如果\(s_i==1\)使得删除一条边之后可以得到一个大小为\(i\)的联通块

数据约束：

\(2 \leq n \leq 10^5\) ，\(s=0或1\)

题解：

显然，如果你能得到\(i\)大小的联通块 那么你肯定可以得到\(n-i\)的联通块。

菊花图。

感觉菊花图好像对于这种构造题有奇效

考虑一个\(m\)个点的菊花图 那么随便怎么切 都只能得到\(m-1\)和1的联通块

如果有一棵大小为\(m_1\)和\(m_2\)的菊花图 将他们合并 变成

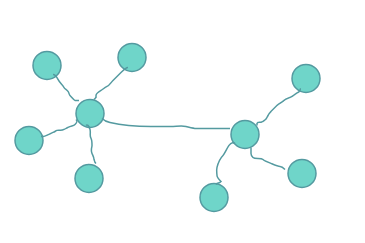
那么我们就可以得到\(m_1-1\)和\(m_2-1\)和\(m_1+m_2-2\)大小的联通块

Code

#include<bits/stdc++.h>
#define fr(i,x,y) for(int i=x;i<=y;++i)
#define rf(i,x,y) for(int i=x;i>=y;--i)
#define LL long long
using namespace std;
const int N=1e5+10;
char lx[N];

int main(){
    scanf("%s",lx+1);
    int n=strlen(lx+1);
    if(lx[n]=='1'||lx[1]=='0'||lx[n-1]=='0') return printf("-1\n"),0;
    fr(i,1,n/2) if(lx[i]!=lx[n-i]) return printf("-1\n"),0;
    int nw=2,rt=2,nm=1;
    printf("1 2\n");
    fr(i,2,n/2){
        if(lx[i]=='1'){
            printf("%d %d\n",++nw,rt);
            rt=nw;
        } else printf("%d %d\n",++nw,rt);
        nm++;
    }
    fr(i,nm+1,n-1) printf("%d %d\n",++nw,rt);
    return 0;
}

---

D.Distance Sums

题意：

给你一个\(n\)个数的数组\(d[]\) , 请你构造一个\(n\)个节点的树 使得满足

• 节点从1标号到\(n\)
• 对于一个节点\(i\) 树上所有节点到\(i\)的距离之和为\(d[i]\)（每条边的长度为1

数据约束：

\(2 \leq n \leq 10^5\) ，\(1 \leq d_i \leq 10^{12}\)

题解：

首先叶子节点的\(d\)值肯定是坠大的嘛QwQ..这点应该没有任何问题

然后就是根据一个被某位神仙d成显然的性质

对于\((u,v)\) \(u\)有一条边连向\(v\)

那么有 \(d[u]+sz[u]-(n-sz[u])==d[v]\)

\(\Rightarrow\) \(u\)的他的父亲是谁啦~

最后不要忘记判一下根节点是否满足条件哦~

Code

#include<bits/stdc++.h>
#define fr(i,x,y) for(int i=x;i<=y;++i)
#define rf(i,x,y) for(int i=x;i>=y;--i)
#define LL long long
using namespace std;
const int N=1e5+10;
struct data{
    int nt,to;
}a[N<<1];
map<LL,int>ys;
int cnt=0,head[N],sz[N];
LL d[N],dis[N];

template <class T>
void read(T &x){
    char ch=getchar();x=0;
    for(;ch<'0'||ch>'9';ch=getchar()) ;
    for(;ch>='0'&&ch<='9';ch=getchar()) x=(x<<1)+(x<<3)+(ch^48);
}

void add(int x,int y){
    a[++cnt].to=y,a[cnt].nt=head[x],head[x]=cnt;
    a[++cnt].to=x,a[cnt].nt=head[y],head[y]=cnt;
}

void fail(){
    printf("-1\n");
    exit(0);
}

void dfs(int u,int fa){
    for(int i=head[u];i;i=a[i].nt){
        if(a[i].to==fa) continue;
        dis[a[i].to]=dis[u]+1;
        dfs(a[i].to,u);
    }
}

int main(){
    int n;read(n);
    fr(i,1,n) read(d[i]),ys[d[i]]=i;
    sort(d+1,d+1+n);
    fr(i,1,n) sz[i]=1;
    rf(i,n,2){
        int u=ys[d[i]];
        int gg=n-2*sz[u];
        if(gg<0) fail();
        LL pos=d[i]-gg;
        if(!ys.count(pos)) fail();
        sz[ys[pos]]+=sz[u];
        add(ys[pos],u);
    }
    dfs(ys[d[1]],0);
    fr(i,1,n) d[1]-=dis[i];
    if(d[1]) fail();
    fr(u,1,n){
        for(int i=head[u];i;i=a[i].nt){
            if(i&1) printf("%d %d\n",a[i].to,u);
        }
    }
    return 0;
}

---