求n位水仙花数

求n位水仙花数

A.两个关键

1.n位水仙花数的范围是什么？

n位水仙花数的范围是[10^n-1,10ⁿ)

2.如何判断是否为水仙花数

核心操作:

2-1.如何得到每一位？

A.核心思想

对得到的数进行先取余后取整的循环操作。

B.具体操作

用一变量g来得到将要判断的值,用变量h来依次存放每一位,g取余后把值赋给变量h，然后g再进行除10运算,如此循环往复,直到h依次得到每一位为止。

2-2.如何将得到的每一位进行n次方？

A.核心思想

调用Math.pow()函数即可(注:Math.pow()函数的返回值是double类型的数据)

B.具体操作

设一个变量t来求和,把操作1的变量h应用Math.pow()函数并把其应用后的值加入到t中,然后循环往复,直到结束该循环。(注:因为水仙花数一般是定义成int类型,所以在赋值运算过程中要把Math.pow()函数得到的值进行强制类型转换)

B.易错点分析

1.Math.pow()函数的返回值是double类型,

a.在赋值运算中,若赋给非double类型的值时都必须执行强制类型转化操作(目的:转换成相同类型)。

b.在比较运算中,系统会自动执行自动类型转化操作(转换方向:级别更高的类型),此时无需执行强制类型转化操作。

2.用来求和的变量t在每次判断完(是否是水仙花数)之后都需要归零。

3.必须用一个新的变量(本题为g)来存放将要判断的值。

C.代码以及运行结果截图

代码截图

运行结果截图

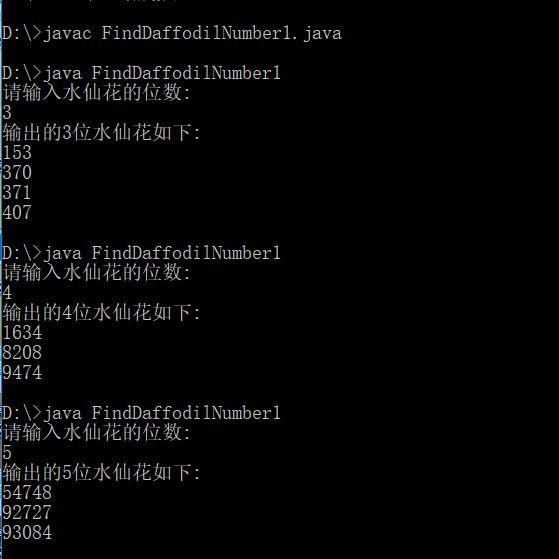
D.所写程序的优缺点

优点:适用范围较广,可以根据用户的需要来进行键盘输入

缺点;运行所花时间有点长而且数据够大时运行不了（其程序运行时占的内存空间不小）

E.相关英语词汇积累

1.水仙花: daffodil; narcissistic;其别名: 自恋数、自幂数或阿姆斯壮数（Armstrong number）.

2.数;number;

3.归零: return to zero。

4.核心思想:core thought.

5.位数: places

6.易错分析:Easy to fault analysis

7.[计] totalizer 加法计算器；

8.[计] accumulator 蓄电池；[计] 累加器；积聚者；

9.[计] assignment operation赋值运算

10.[计] comparison operation比较运算