【NOIP2014提高组】联合权值

https://www.luogu.org/problem/show?pid=1351

既然是一棵树，就先转化成有根树。有根树上距离为2的点对，路径可能长下面这样：

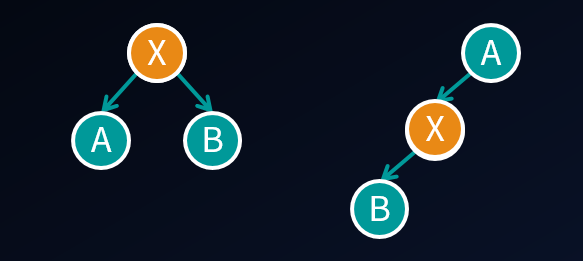
枚举路径上的中间点X。

第一种情况

对于点X（X的儿子数≥2），它的每一个儿子i与其他的儿子对权值和的贡献为W_i*(sum-W_i)，则这个点所有儿子之间对权值和的贡献为：∑W_i*(sum-W_i)，其中sum为点X所有儿子的权值之和。（貌似还有更高效的算法？）

对于点X （X的儿子数≥2），它的所有儿子之间可以产生的联合权值的最大值，肯定为所有儿子里面权值最大的×权值第二大的。贪心即可。

第二种情况

对于点X（除根节点和叶子节点），它的父亲与它的所有儿子之间对权值和的总贡献为：2*W_father*sum，其中sum为点X所有儿子的权值之和。因为要求的是有序点对，所以要乘2。

对于点X（除根节点和叶子节点），它的父亲与它的所有儿子之间产生的联合权值的最大值，肯定为它的儿子里面权值最大的乘以它的父亲的权值。贪心即可。

实际代码时发现不用特意转化为有根树，只需要一遍深搜。

对于每个点，判断它的儿子数时，如果不是根则等于这个点的度数-1，如果是根则等于这个点的度数。

统计每个点对权值和的贡献，并维护最大权值。

#include <iostream>
#include <vector>
#define maxn 200005
typedef long long llint;
using namespace std;
const llint inf = 0x7fffffffffffffffll, c = ;
int n;
vector<int> t[maxn];
llint weight[maxn];
llint tot = ;
llint maxlink = -inf;
void dfs(int k, int fa)
{
    llint sum = ;
    llint maxson[] = {-inf, -inf};
    for (int i = ; i < t[k].size(); i++)
    {
        if (t[k][i] != fa)
        {
            sum = (sum + weight[t[k][i]]) % c;
            if (weight[t[k][i]] > maxson[])
            {
                maxson[] = maxson[];
                maxson[] = weight[t[k][i]];
            }
            else if (weight[t[k][i]] > maxson[])
            {
                maxson[] = weight[t[k][i]];
            }
            dfs(t[k][i], k);
        }
    }
    if (t[k].size() >=  + (fa !=  ?  : ))
    {
        for (int i = ; i < t[k].size(); i++)
            if (t[k][i] != fa)
                tot = (tot + (sum - weight[t[k][i]] + c) % c * weight[t[k][i]] % c) % c;
        // tot = tot + (sum - weight[t[k][i]]) * weight[t[k][i]]
        maxlink = max(maxlink, maxson[] * maxson[]);
    }
    if (fa !=  && t[k].size() >= )
    {
        tot = (tot +  * weight[fa] % c * sum % c) % c;
        maxlink = max(maxlink, maxson[] * weight[fa]);
    }
}
int main()
{
    int a, b;
    cin >> n;
    for (int i = ; i < n; i++)
    {
        cin >> a >> b;
        t[a].push_back(b);
        t[b].push_back(a);
    }
    for (int i = ; i <= n; i++)
    {
        cin >> weight[i];
    }
    dfs(, );
    cout << maxlink << ' ' << tot << endl;
    return ;
}