python函数（4）：递归函数及二分查找算法

人理解循环，神理解递归！

 

本篇导航：

• 递归的定义
• 二分查找算法

一、递归的定义

def story():
    s = """
    从前有个山，山里有座庙，庙里老和尚讲故事，
    讲的什么呢？
    """
    print(s)
    story()

story()

老和尚讲故事

递归的定义——在一个函数里再调用这个函数本身。这种魔性的使用函数的方式就叫做递归。

递归的最大深度：997

1、python递归最大层数限制 997

2、最大层数限制是python默认的，可以做修改

3、但是我们不建议你修改

n = 0
def f():
    global n
    n += 1
    print(n)
    f()

f()

测试递归最大深度

如何修改递归最大深度：

import sys #所有和python相关的设置和方法
sys.setrecursionlimit(10000000)
n = 0
def f():
    global n
    n += 1
    print(n)
    f()

f()

修改递归最大深度

递归的小实践：

1、猜年龄：

#猜e的年龄
#e比d大两岁
#d比c大两岁
#c比b大两岁
#b比a大两岁
#a 40了

# 1.a  age(1) = 40
# 2.b  age(1) + 2
# 3.c   age(2) + 2
# 4.d  age(3) + 2
# 5.e  age(4) + 2

def age(n):
    if n == 1:
        return 40
    else:
        ret = age(n-1)
        return ret + 2
age(5)

猜年龄

2、一个数，除2到不能整除2为止：

#一个数，除2到不能整除2为止（以8为例）
def cal(num):
    if num % 2 == 0:
        num  = num // 2
        return cal(num)
    else:
        return num

print(cal(8))

数字整除类1

3、整除类2

#如果一个数 可以整除2 就整除
#不能整除就*3+1
def func(num):
    print(num)
    if num == 1:
        return
    if num %2 == 0:
        num = num //2
    else:
        num = num * 3 + 1
    func(num)

func(5)

数字整除类2

递归函数与三级菜单

menu = {
    '北京': {
        '海淀': {
            '五道口': {
                'soho': {},
                '网易': {},
                'google': {}
            },
            '中关村': {
                '爱奇艺': {},
                '汽车之家': {},
                'youku': {},
            },
            '上地': {
                '百度': {},
            },
        },
        '昌平': {
            '沙河': {
                '老男孩': {},
                '北航': {},
            },
            '天通苑': {},
            '回龙观': {},
        },
        '朝阳': {},
        '东城': {},
    },
    '上海': {
        '闵行': {
            "人民广场": {
                '炸鸡店': {}
            }
        },
        '闸北': {
            '火车战': {
                '携程': {}
            }
        },
        '浦东': {},
    },
    '山东': {},
}

def threeLM(dic):
    while True:
        for k in dic:print(k)
        key = input('input>>').strip()
        if key == 'b' or key == 'q':return key
        elif key in dic.keys() and dic[key]:
            ret = threeLM(dic[key])
            if ret == 'q': return 'q'
        elif (not dic.get(key)) or (not dic[key]) :
            continue

threeLM(menu)

递归函数实现三级菜单

---

二、二分查找算法

给你一个数列让你找出其中一个数的位置你怎么找？index？这是python给我们的内置函数。那他内部是怎么实现的呢？现在要求我们自己设计函数来实现这个功能。

数列例如：l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]

l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]

i = 0
for num in l:
    if num == 66:
        print(i)
    i+=1

是不是感觉这个函数so easy但是我们所用的方法是循环列表然后一个一个对比。这个方法固然可以可是也只是适用于小的数组。如果这个数列很长里面上万甚至更多，一个一个找效率太低。必须有一个新的算法来解决这个问题。这就引出了今天另一个知识点二分查找

二分查找算法:

算法：计算的方法

二分查找前提：有序的递增列表

图示：

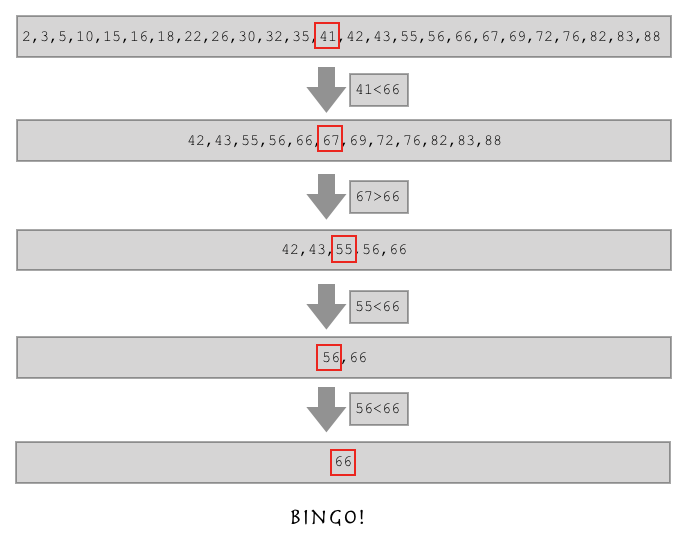
这就是二分查找算法

简单二分法：

l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]

def func(l,aim):
    mid = (len(l)-1)//2
    if l:
        if aim > l[mid]:
            func(l[mid+1:],aim)
        elif aim < l[mid]:
            func(l[:mid],aim)
        elif aim == l[mid]:
            print("bingo",mid)
    else:
        print('找不到')
func(l,66)
func(l,6)

二分法基础版

二分法升级：

def func(l, aim,start = 0,end = len(l)-1 ):
    mid = (start+end)//2
    if not l[start:end+1]:
        return
    elif aim > l[mid]:
        return func(l,aim,mid+1,end)
    elif aim < l[mid]:
        return func(l,aim,start,mid-1)
    elif aim == l[mid]:
        print("bingo")
        return mid

index = func(l,68)
print(index)

二分法查找升级版

小结：

递归解决的问题：

就是通过参数，来控制每一次调用缩小计算的规模

适合的场景：

数据的规模在减小，但是解决问题的思路没有改变

结束递归的标志：return

---

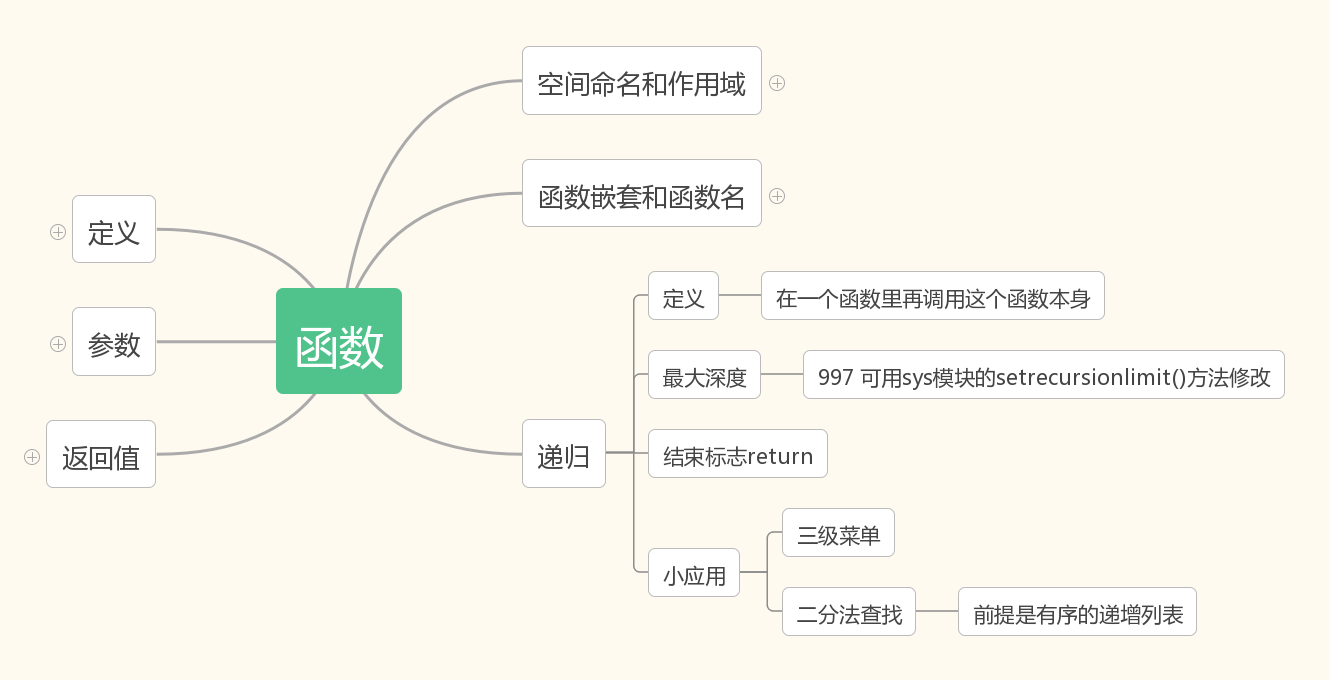
思维导图：