Tesseract环境搭建及编译安装

Tesseract环境搭建及编译安装

Tesseract源码都是C++源码；对于不咋会C++的人来说，这真是。。。虽然说语言有相通性，但是。。。哎！！！！！

分享出来，也希望对大家有所帮助。

环境：win10系统，vs2017

（注：安装vs2017,在vs2017 installer  C++的桌面开发下可选插件选择windows 10 SDK(有多个版本，不知道的情况下选择第一个,防止编译的时候找不到所需要的一些东西）

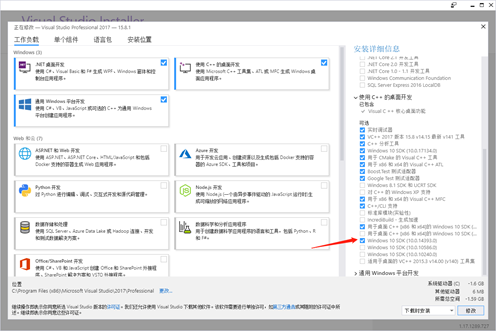
个人理解：cppan：类似于java的maven,负责管理包；

1.path下添加vs2017的路径（默认安装，路径在：C:\Program Files (x86)\Microsoft Visual Studio\2017\Professional\Common7\IDE）

2.cppan、cmake下载安装，配置path（下载最新的，https://cppan.org/client/；https://cmake.org/download/）

3.打开dos，执行cppan --build pvt.cppan.demo.google.tesseract.tesseract-master；(需要FQ，有些包下载不下来)

4.下载tesseract 源码；（https://github.com/tesseract-ocr）

5.dos命令下进入到tesseract源码文件夹下，执行cppan （下载依赖的包；FQ；有的包下载不下来）

Dos下编译：

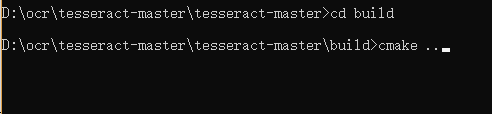
6.在tesseract根目录下新建文件夹build，并进入到build中；mkdir build && cd build

7. cmake ..  (后面俩点是必要的，默认是win32,x64需要指定)

cmake .. -G "Visual Studio 14 2015 Win64" -DCMAKE_PREFIX_PATH="D:\orc"
cmake .. -G "Visual Studio 14 2015"
-DCMAKE_PREFIX_PATH="D:\orc"

解释：

.. 向上一层目录
-G 后面跟指定的编译器
-DCMAKE_PREFIX_PATH= 指定编译器所在目录

8.cmake完成之后，会在build目录下有一个tesseract.sln文件，以管理员权限打开vs2017,并打开tesseract.sln文件；解决方案资源管理器中就是c++ 使用CMake生成vs项目

9.编译没有问题后，在“解决方案资源管理器”中点选“解决方案 tesseract”–>“CMakeTargets”–>“INSTALL”，单击右键，在出现的菜单中选择“生成”。

Debug和release模式下需要分别执行上述步骤；

在C:\Program Files
(x86)目录下，就会有tesseract的文件，dos进入C:\Program Files (x86)\tesseract目录，输入tesseract,可以验证该版本

值得注意的地方是，即使你这么做了，也是要看运气的哦，就怕你所需要的包没有下载下来

(参考：https://github.com/tesseract-ocr/tesseract/wiki/Compiling#windows，

https://blog.csdn.net/naidoudou/article/details/70225849，

https://blog.csdn.net/qq_29473063/article/details/80621115

)