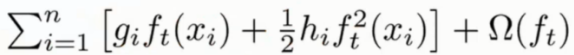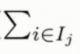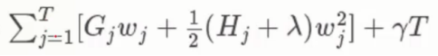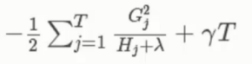工作原理

基于集成算法的多个树累加, 可以理解为是弱分类器的提升模型

公式表达

基本公式

目标函数

目标函数这里加入了损失函数计算

这里的公式是用的均方误差方式来计算

最优函数解

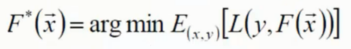
要对所有的样本的损失值的期望, 求解最小的程度作为最优解

集成算法表示

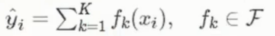
集成算法中对所有的树进行累加处理

公式流程分解

每加一棵树都应该在之前基础上有一个提升

损失函数

叶子节点惩罚项

损失函数加入到基本公式目标函数中

多余出来的常数项就用 c 表示即可

目标函数推导

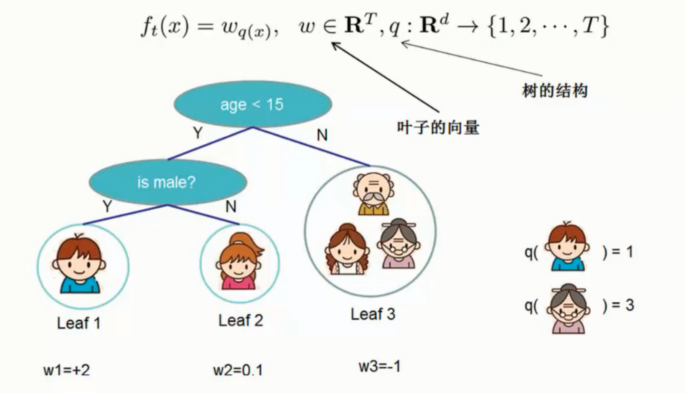
如上图. 三个树, 真实值 1000 , 第一棵树预测950, 残差 50

第二颗就预测 30, 残差 20 , 一次类推最终结果预测 995

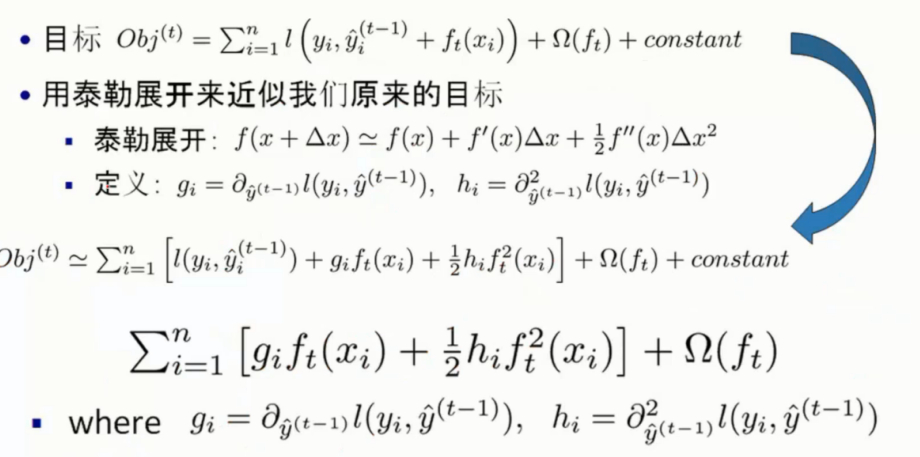
这里拟定近似成为了泰勒展开的形式

然后优化的时候, 对于  是对上一颗树的结果, 这个值对于下面是不会变动的

因此可以视为常数, 和最后面的常数项合并省略掉了

然后 gi 表示一阶导, hi 表示二阶导

去除掉常数项对极值不会有影响后

就剩下了 

继续化简,   带入

 是对样本的遍历, 这样的话感觉和后面的 T 关系不大

在物理意义上所有的样本点都是会落到叶子节点上的

因此遍历样本和遍历叶子节点都是全部遍历到的

于是这里转换成对叶子节点的遍历 

对于每一个叶子节点则需要再遍历一次这个叶子节点上的所有样本 

而包含有 w2j   的两项可以进行合并从而得到了

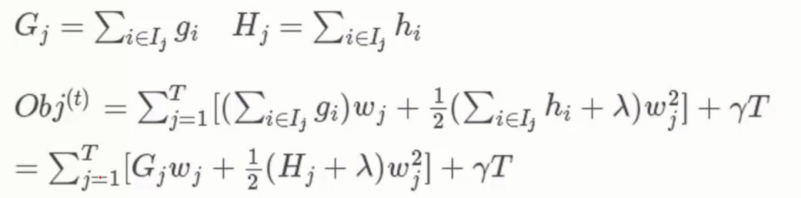
里面每个叶子节点的导数求和分别用 Gj 和 Hj 来表示一阶和二阶

从而进一步的化简得到最终的 目标函数

目标函数求解

怎么样的 wj 可以让目标函数最小? 依旧是对 wj 偏导

然后求导等于0获得 wj 的表达式带入原函数

得最终解

其中对每一个Hj 和 Gj 都是可以得出的

以及 T 叶子节点数和 λ 都是已知的

目标函数使用实例

实际的操作中即可计算出每个叶子节点的一阶导二阶导

如果叶子中只有一个样本就按唯一的来算

多个就累加处理即可

而目标函数的的值越小则表示树结构越优

相比较之前的用熵值进行计算, 这里可以直接使用我们的目标函数的解来衡量判断模型

根据我们根据现有模型的值减去随机分割的左子树的值和右子树的值

然后这个值越大表示这时候的增益是最大的, 因此可以判断在哪里切是最优的

机器学习 - 算法 - Xgboost 数学原理推导的更多相关文章

  1. PCA主成分分析算法的数学原理推导

    PCA(Principal Component Analysis)主成分分析法的数学原理推导1.主成分分析法PCA的特点与作用如下:(1)是一种非监督学习的机器学习算法(2)主要用于数据的降维(3)通 ...

  2. SVM数学原理推导

    //2019.08.17 #支撑向量机SVM(Support Vector Machine)1.支撑向量机SVM是一种非常重要和广泛的机器学习算法,它的算法出发点是尽可能找到最优的决策边界,使得模型的 ...

  3. opencv——PCA（主要成分分析）数学原理推导

    引言: 最近一直在学习主成分分析(PCA),所以想把最近学的一点知识整理一下,如果有不对的还请大家帮忙指正,共同学习. 首先我们知道当数据维度太大时,我们通常需要进行降维处理,降维处理的方式有很多种, ...

  4. SVM数学原理推导&鸢尾花实例

    //看了多少遍SVM的数学原理讲解,就是不懂,对偶形式推导也是不懂,看来我真的是不太适合学数学啊,这是面试前最后一次认真的看,并且使用了sklearn包中的SVM来进行实现了一个鸢尾花分类的实例,进行 ...

  5. Dijkstar算法的数学原理

    Dijkstar算法是荷兰数学家迪克斯屈拉(or迪杰斯特拉?)在1959年发现的一个算法.是现有的几个求带权图中两个顶点之间最短通路的算法之一.算是一个相当经典的算法了. 迪克斯屈拉算法应用于无向连通 ...

  6. [杂记]对RSA算法的数学原理的一点思考

  7. DH算法图解+数学证明

    前几天和同事讨论IKE密钥交换流程时,提到了Diffie-Hellman交换.DH算法最主要的作用便是在不安全的网络上成功公共密钥(并未传输真实密钥).但由于对于DH算法的数学原理则不清楚,因此私下对 ...

  8. Spark Mllib里的协调过滤的概念和实现步骤、LS、ALS的原理、ALS算法优化过程的推导、隐式反馈和ALS-WR算法

    不多说,直接上干货! 常见的推荐算法 1.基于关系规则的推荐 2.基于内容的推荐 3.人口统计式的推荐 4.协调过滤式的推荐 (广泛采用) 协调过滤的概念 在现今的推荐技术和算法中,最被大家广泛认可和 ...

  9. 【机器学习笔记之七】PCA 的数学原理和可视化效果

    PCA 的数学原理和可视化效果 本文结构: 什么是 PCA 数学原理 可视化效果 1. 什么是 PCA PCA (principal component analysis, 主成分分析) 是机器学习中 ...

随机推荐

  1. WebClient 与HttpClient 的区别

    需要搜索下资料. -------------------------------------------------- 微软文档介绍,新的开发中推荐使用:HttpClient WebClient 文档 ...

  2. linux下解决find 1000/gfs无权限

    用find查找根目录下的文件时,比如sudo find . -name \*test,就会出现1000/gfs无权限的情况 用一下方法可以正常使用 sudo find . -name test 2&g ...

  3. 什么是Log4j，Log4j详解！

    由于时间紧急,自己就不写了.一下转载链接: https://www.cnblogs.com/ITtangtang/p/3926665.html

  4. 在virtualenv中使用不同的Python版本

    来源:百度SEO公司   我有一个目前使用python 2.5.4运行的Debian系统. 我正确安装了virtualenv,一切正常. 我是否可以将virtualenv与其他版本的Python一起使 ...

  5. python导包问题，这一篇就够了

    解决办法: 将项目所在的根目录添加到sys.path中 在入口文件中加入如下代码: import sys import os # 将 项目的根目录添加到sys.path中 BASE_DIR = os. ...

  6. docker学习（六）

    一.Dockerfile使用 Dockerfile 可以允许用户创建自定义的镜像. 1.基本结构Dockerfile 由一行行命令语句组成,并且支持以 # 开头的注释行.一般的,Dockerfile ...

  7. json与java bean对象转换

    第一步:引入fastjson的依赖jar包 注:如果引入此版本的依赖,导致项目不能启动(报错:找不到启动类);那么可以换一个版本的fastjson即可. 给出文字版: <!-- fastjson ...

  8. HR#7 题解

    T1 签到题 #include<bits/stdc++.h> #define R register int using namespace std; inline int g() { R ...

  9. 使用webuploader实现分片上传

    这里只写后端的代码,基本的思想就是,前端将文件分片,然后每次访问上传接口的时候,向后端传入参数:当前为第几块文件,和分片总数 下面直接贴代码吧,一些难懂的我大部分都加上注释了: 上传文件实体类: 看得 ...

  10. vue 组件的通信方式（完整版）

    几种通信方式无外乎以下几种: Prop(常用) $emit (组件封装用的较多) .sync语法糖 (较少) $attrs & $listeners (组件封装用的较多) provide &a ...