P1282 多米诺骨牌[可行性01背包]

题目来源：洛谷

题目描述

多米诺骨牌有上下2个方块组成，每个方块中有1~6个点。现有排成行的

上方块中点数之和记为S1，下方块中点数之和记为S2，它们的差为|S1-S2|。例如在图8-1中，S1=6+1+1+1=9，S2=1+5+3+2=11，|S1-S2|=2。每个多米诺骨牌可以旋转180°，使得上下两个方块互换位置。 编程用最少的旋转次数使多米诺骨牌上下2行点数之差达到最小。

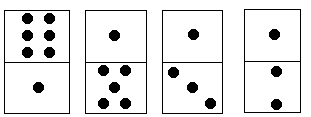
对于图中的例子，只要将最后一个多米诺骨牌旋转180°，可使上下2行点数之差为0。

输入输出格式

输入格式：

输入文件的第一行是一个正整数n(1≤n≤1000)，表示多米诺骨牌数。接下来的n行表示n个多米诺骨牌的点数。每行有两个用空格隔开的正整数，表示多米诺骨牌上下方块中的点数a和b，且1≤a，b≤6。

输出格式：

输出文件仅一行，包含一个整数。表示求得的最小旋转次数。

输入输出样例

输入样例#1：

4
6 1
1 5
1 3
1 2

输出样例#1：

1

解析：

灰常好的一道高质量题目。通过这道题，可以让你稍稍理解到背包问题的本质。

---

【可行性背包】

看到其他地方上没什么人讲，实际上这也是一个衍生出来的背包问题，模板题参见 poj1742。

 

具体什么是可行性背包，按照我个人理解，实质上就是在每一个新物品加入背包时，更新之前的状态能转移到当前状态的状态，其他状态不转移。

我们知道，背包问题一般有一个背包容量W，一些物品体积V1~Vn，以及这些物品对应的价值C1~Cn。

对于可行性背包，实际上我们是对整个背包容量W进行了一次遍历，寻找可以放置下一个物品的位置，然而由于这些物品的某些性质，使得对于容积为W的背包的某个容量wi，所有放置物品的方案都无法使容积到达wi。

比如我们有体积为2，5，6，10的四个物品和一个容积为20的背包，那么显然这个背包不可能只装体积为1的物品。

 

也就是说，对于每一个要放进背包的物品，我们都要检查一遍从各个状态能否转移到当前状态。

 

这就是背包的本质：每一个物品或动作对所有当前状态的更新。对于不可行的解，我们排除之，对于可行解，我们求之。

 

对于这道题，确实比较难看出可行性背包，而且状态设计也是个难点，更别说那个该死的绝对值。。。

我们一一解决它们。

 

首先对于这个绝对值，我们可以发现一个规律：对于一组数据，无论怎么反转牌，它们的点数总和相等。

很容易就想到对于任意的1~i个牌，点数总和减去上面的1~i个牌的点数和就是下面对应的1~i个牌的点数和。

绝对值可解，我们只要想办法把其中一行的最优解求出来，下面那一行就是可导的。

 

状态设计是最苟的。如果你之前没做过可行性背包，那就会像我一样想一个晚上也想不出来正解，倒是贪心啊暴力啥的解法往脑子里蹦。

为什么我们那可行性背包来做？首先是这个题满足一个背包的本质要求，就是使某个属性最优时，另一个属性的最优情况，在这道题里面最优就是上下差值最小时的最小转动次数。然后就是因为我们有很多不同的装入背包方案，然而我们并不知道：1、哪一种是最优 2、哪一种可以通过翻转转出来。而且这明显是需要一个约束，即上下差值最小时的最小转动次数。

 

我们假设dp[i][j]表示转动第i个牌时，上面那一行总和为j时的最小转动次数（这是可行性背包的模板，好好理解这个j），对于每次“加入"背包的牌，我们有翻转和不翻转两种决策，没转就继承上一个状态，转了就把次数加一。

 

状态转移方程：

if(j>=a[i]) dp[i][j]=min(dp[i][j],dp[i-1][j-a[i]]);//不转
if(j>=b[i]) dp[i][j]=min(dp[i][j],dp[i-1][j-b[i]]+1);//转动

初始状态：

假设上面那一排的输入数据为up[]，下面那一行为down[]；

如果第一个牌上下不等，那么就是dp[1][up[1]]=0，dp[1][down[1]]=1，也就是最开始可以把下面的牌转动到上面；

如果第一个牌上下相等，就是dp[1][up[1]]=dp[1][down[1]]=0，就是转不转都一样嘛。

很好，由于是可行性背包，现在我们只需要注意一下背包容量也就是状态大小到达了6*n，就是最大总和。

完事。

参考代码：

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<cmath>
 #include<algorithm>
 #include<string>
 #include<cstdlib>
 #include<queue>
 #include<vector>
 #define INF 0x3f3f3f3f
 #define PI acos(-1.0)
 #define N 1010
 #define MOD 2520
 #define E 1e-12
 using namespace std;
 int dp[N][N*],a[N],b[N],cnt;
 int main()
 {
     int n;
     cin>>n;
     for(int i=;i<=n;i++)
         scanf("%d%d",&a[i],&b[i]),cnt+=a[i]+b[i];
     memset(dp,0x3f,sizeof(dp));
     if(a[]!=b[]) dp[][a[]]=,dp[][b[]]=;
     else dp[][a[]]=0,dp[][b[]]=0;
     //对于任意一个牌i，到i的可能的和可以达到6*n
     //状态设计为dp[i][j]表示到第i个牌，若上面那一行的总和为j时所能得到的最少转动次数
     for(int i=;i<=n;i++)
      for(int j=;j<=*n;j++){
          if(j>=a[i]) dp[i][j]=min(dp[i][j],dp[i-][j-a[i]]);//不转
          if(j>=b[i]) dp[i][j]=min(dp[i][j],dp[i-][j-b[i]]+);//转动
      }

     int minc=INF,ans=INF;//minc最小差值，ans最小交换次数
     for(int i=;i<=cnt;i++){
         if(dp[n][i]<INF){//如果总和为i的情况存在
             if(abs(i-(cnt-i))<minc){//记下最小差值和最小交换次数
                 minc=abs(i-(cnt-i));ans=dp[n][i];
             }
             else if(abs(i-(cnt-i))==minc)//在最小差值最小时，还要比较交换次数
                 ans=min(ans,dp[n][i]);
         }
     }
     cout<<ans<<endl;
     return ;
 }