自由度为n的卡方分布χ²(n)的期望等于n、方差等于2n的证明

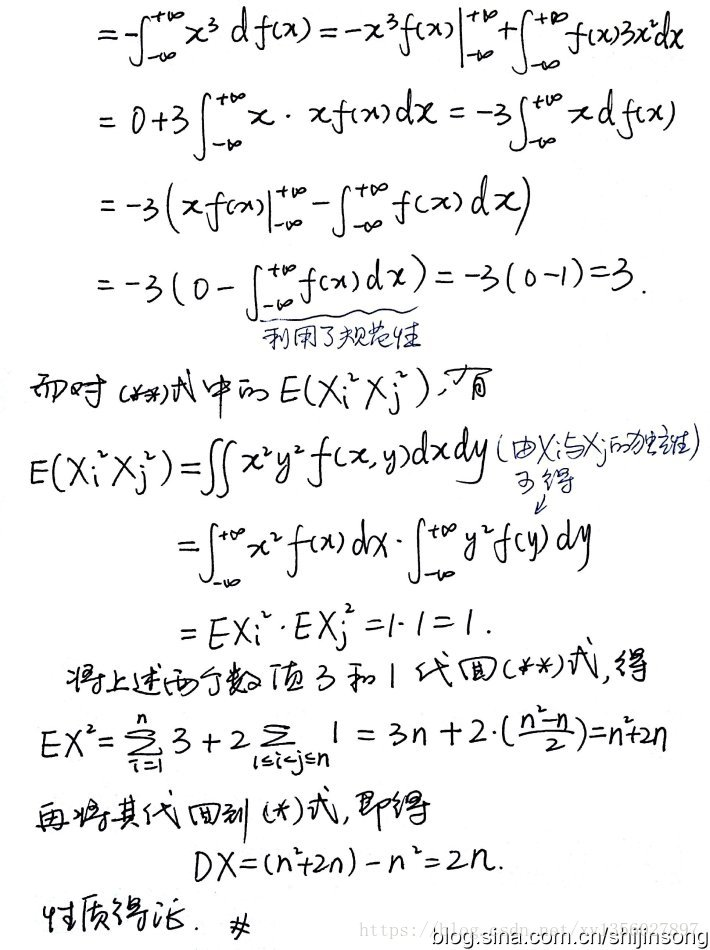
出自:http://blog.sina.com.cn/s/blog_4cb6ee6c0102xh17.html
自由度为n的卡方分布χ²(n)的期望等于n、方差等于2n的证明的更多相关文章
- 卡方分布(Chi-Square Distribution):
定义:如果我们的随机变量是标准正态分布(详见以前博客的高斯分布),那么多个随机变量的平方和服从的分布即为卡方分布. X=Y12+Y22+⋯+Yn2 其中,Y1,Y2,⋯,Yn均为服从标准正态分布的随机 ...
- SLAM中的卡方分布
视觉slam中相邻帧特征点匹配时,动辄上千个特征点,匹配错误的是难免的,而误匹配势必会对位姿精度以及建图精度造成影响,那么如何分辨哪些是误匹配的点对儿呢?如果已知两帧的的单应矩阵,假设单应矩阵是没有误 ...
- spark MLlib 概念 3: 卡方分布(chi-squared distribution)
数学定义[编辑] 若k个随机变量.--.是相互独立,符合标准正态分布的随机变量(数学期望为0.方差为1),则随机变量Z的平方和 被称为服从自由度为 k 的卡方分布,记作 Definition[edit ...
- 样本方差的抽样分布 χ2(n) 卡方分布_样本方差 卡方分布
样本方差的抽样分布 χ2(n) 卡方分布_样本方差 卡方分布 样本方差的抽样分布 χ2(n) 卡方分布 t分布.卡方分布.f分布均要求总体服从正态分布. 若n个相互独立的随机变量ξ1,ξ2,-,ξn ...
- 2018.08.30 bzoj4318: OSU!(期望dp)
传送门 简单期望dp. 感觉跟Easy差不多,就是把平方差量进阶成了立方差量,原本维护的是(x+1)2−x2" role="presentation" style=&qu ...
- 【BZOJ】4318: OSU! 期望DP
[题意]有一个长度为n的01序列,每一段极大的连续1的价值是L^3(长度L).现在给定n个实数表示该位为1的概率,求期望总价值.n<=10^5. [算法]期望DP [题解]后缀长度是一个很关键的 ...
- 【洛谷1654/BZOJ4318】OSU!(期望DP)
题目: 洛谷1654 分析: 本人数学菜得要命,这题看了一整天才看明白-- 先说说什么是"期望".不太严谨地说,若离散型随机变量(可以看作"事件")\(X\)取 ...
- 概率与期望详解!一次精通oi中的概率期望
目录 基础概念 最大值不超过Y的期望 概率为P时期望成功次数 基础问题 拿球 随机游走 经典问题 期望线性性练习题 例题选讲 noip2016换教室 区间交 0-1边树求直径期望 球染色 区间翻转 二 ...
- bzoj3270 博物馆(期望+高斯消元)
Time Limit: 30 Sec Memory Limit: 128 MB 有一天Petya和他的朋友Vasya在进行他们众多旅行中的一次旅行,他们决定去参观一座城堡博物馆.这座博物馆有着特别的 ...
随机推荐
- 查看是否用GPU跑的TensorFlow程序
查看是否用GPU跑的TensorFlow程序 第一种方法,直接输出日志法(推荐) import tensorflow as tf sess = tf.Session(config=tf.ConfigP ...
- Redis05——Redis高级运用(管道连接,发布订阅,布隆过滤器)
Redis高级运用 一.管道连接redis(一次发送多个命令,节省往返时间) 1.安装nc yum install nc -y 2.通过nc连接redis nc localhost 6379 3.通过 ...
- 小程序UI设计(10)-巧用模板,事半功倍
工具中为小程序员们准备了符合微信开发规范的模板.之前帖子中介绍的规范都在模板中已经设计好了,可以直接复制粘贴使用.下图中的样式是从模板直接复制过来的.实际使用时只要更换为自己的图片和文字即可.自动生成 ...
- Acwing 197. 阶乘分解
给定整数 N ,试把阶乘 N! 分解质因数,按照算术基本定理的形式输出分解结果中的 pipi 和 cici 即可. 输入格式 一个整数N. 输出格式 N! 分解质因数后的结果,共若干行,每行一对pi, ...
- python中ord()函数,chr()函数,unichr()函数
ord()函数,chr()函数,unichr()函数 chr()函数用一个范围在range(256)内的(就是0-255)整数作参数,返回一个对应的字符.unichr()跟它一样,只不过返回的是Uni ...
- markdown 使用总结
Markdown介绍 Markdown 是一种轻量级标记语言,创始人为约翰·格鲁伯(John Gruber).它允许人们“使用易读易写的纯文本格式编写文档,然后转换成有效的XHTML(或者HTML)文 ...
- 基于python的爬虫项目
一.项目简介 1.1 项目博客地址 https://www.cnblogs.com/xsfa/p/12083913.html 1.2 项目完成的功能与特色 爬虫和拥有三个可视化数据分析 1.3 项目采 ...
- 「美团 CodeM 资格赛」试题泛做
LibreOJ真是吼啊! 数码 推个式子,把枚举因数转为枚举倍数.然后就发现它是根号分段的.然后每一段算一下就好了. #include <cstdio> #include <cstr ...
- 通过PCI9030向外部RAM写数据失败现象
我们的系统方案是:以9030作为PCI接口芯片,本地端映射了一片IDT70V06的双端口RAM.进行数据传输压力测试时,发现PC机向IDT70V06写数据偶尔会失败.这一问题是什么原因造成的呢? 最初 ...
- ssh以及双机互信
当我们要远程到其他主机上面时就需要使用ssh服务了. 我们就来安装一下sshd服务以及ssh命令的使用方法. 服务安装: 需要安装OpenSSH 四个安装包: 安装包: openssh-5.3p1-1 ...
