Spring Security(1)：认证和授权的核心组件介绍及源码分析

Spring Security是一个能够为基于Spring的企业应用系统提供声明式的安全访问控制解决方式的安全框架。它包括认证（Authentication）和授权（Authorization）两个部分。

用户认证指的是验证某个用户是否为系统中的合法主体，也就是说用户能否访问该系统。用户认证一般要求用户提供用户名和密码。系统通过校验用户名和密码来完成认证过程。用户授权指的是验证某个用户是否有权限执行某个操作。

一般来说，系统会为不同的用户分配不同的角色，而每个角色则对应一系列的权限。   spring security的主要核心功能为认证和授权，所有的架构也是基于这两个核心功能去实现的。

认证的核心组件：

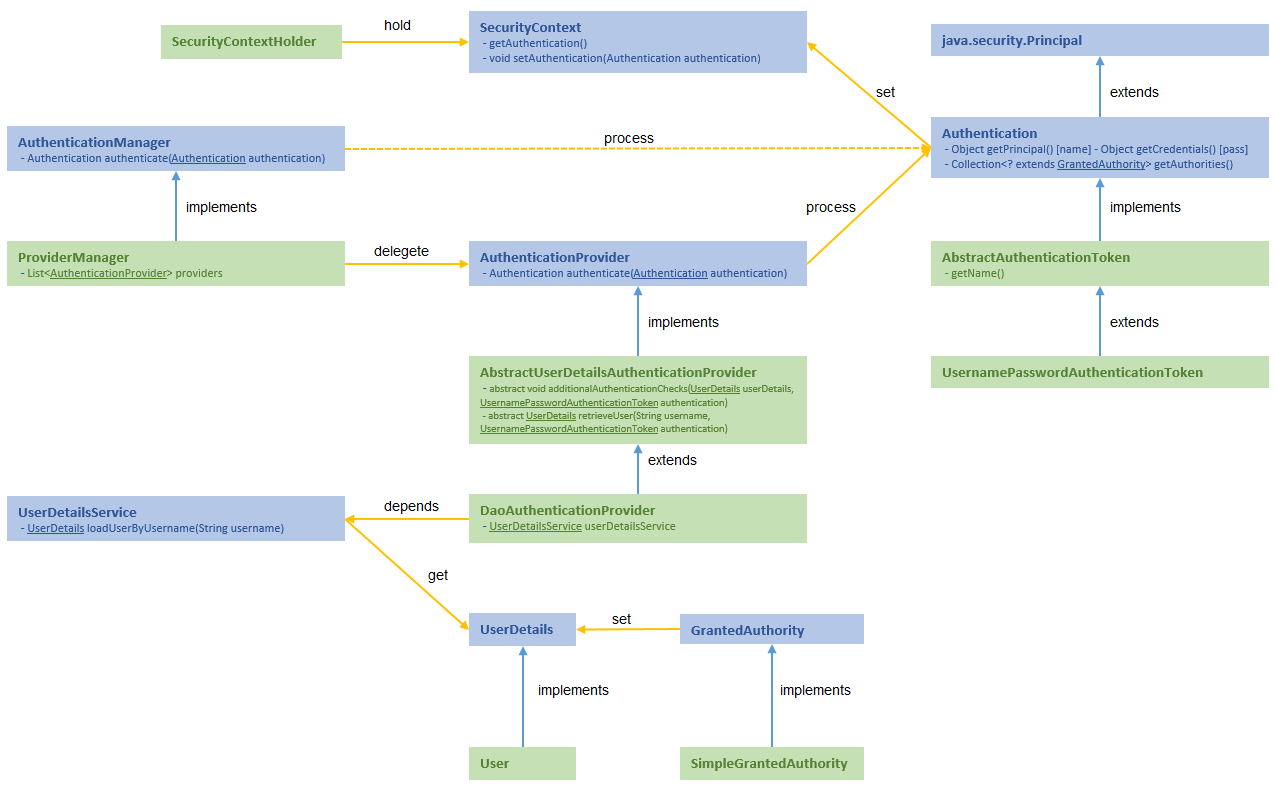
[AuthenticationManager] 是一个接口，是认证方法的入口，定义了如何认证，接收一个Authentication对象作为参数。

[ProviderManager] 是AuthenticationManager的一个默认实现，但它并不用来处理身份认证，而是委托给配置好的AuthenticationProvider。在ProviderManager的authenticate方法中，会轮训成员变量List<AuthenticationProvider> providers。该providers中如果有一个AuthenticationProvider的supports函数返回true，那么就会调用该AuthenticationProvider的authenticate函数认证，如果认证成功则整个认证过程结束。如果不成功，则继续使用下一个合适的AuthenticationProvider进行认证，只要有一个认证成功则为认证成功。

[AuthenticationProvider] 是一个接口，ProviderManager实际上把认证过程委托给了AuthenticationProvider对象（实际上是一个List）来处理。AuthenticationProvider的实现类有很多，如：

DaoAuthenticationProvider  (extends AbstractUserDetailsAuthenticationProvider)：最常用的认证方式，通过UserDetailsService对UserDetails认证。

AnonymousAuthenticationProvider： 用于匿名身份认证，匿名用户名和权限使用默认值为anonymousUser，ROLE_ANONYMOUS

[Authentication] 是一个接口，它定义存储用户的Principal（用户信息），Credentials（密码），Authority（权限）等信息。它将提供这些信息给AuthenticationManager（AuthenticationProvider的各种实现类）进行验证。验证成功后，返回一个认证成功的Authentication的实现类的对象。Authentication的实现类也有很多，并且和AuthenticationProvider对应， 如：

DaoAuthenticationProvider -> UsernamePasswordAuthenticationToken

AnonymousAuthenticationProvider -> AnonymousAuthenticationToken

[UserDetails] 是一个接口，定义了认证所需的必要信息，包括用户名，密码，权限，有效性等。在实际使用里，（比用JPA）通过定义User实体类与DB中的User表和Role表映射实现UserDetails接口。也可以使用框架的User实现类来构造User，比如使用AuthenticationManagerBuilder中的inMemoryAuthentication()方法或jdbcAuthentication()方法获取InMemoryUserDetailsManagerConfigurer或JdbcUserDetailsManagerConfigurer对象来构造。

[SecurityContextHolder] & [SecurityContext] SecurityContextHolder是SecurityContext的存放容器，默认使用ThreadLocal存储，意味SecurityContext在相同线程中的方法都可用。由于SecurityContext中存放有Authentication信息，因此我们可以通过用这种方式在Security上下文中拿到User信息。如：

Object principal = SecurityContextHolder.getContext().getAuthentication().getPrincipal();
if (principal instanceof UserDetails) {
    String username = ((UserDetails)principal).getUsername();
} else {
    String username = principal.toString();
}

以上就是各个接口的意义及关系，认证中其实最重要的就是authenticate()方法的实现。上面也说到，AuthenticationManager把该方法委托给AuthenticationProvider来做，接下来就以AuthenticationProvider的一个最常用的实现类DaoAuthenticationProvider来叙述以下认证过程（具体代码可以从AbstractUserDetailsAuthenticationProvider.authenticate()开始看）：

（1）从request中拿到username和password，存到一个UsernamePasswordAuthenticationToken（Authentication的接口实现类）对象中

（2）开始调用AbstractUserDetailsAuthenticationProvider.authenticate()方法

（3）拿到UsernamePasswordAuthenticationToken的username

（4）调用DaoAuthenticationProvider.retrieveUser()，用步骤3的username，调用UserDetailsService.loadUserByUsername()方法拿到User对象（UserDetails的接口实现类）

（5）检查步骤4中User对象的有效性（enabled，expired，locked）

（6）调用DaoAuthenticationProvider.additionalAuthenticationChecks()，比较UsernamePasswordAuthenticationToken的password和UserDetails的password（都是encoded），一致则通过

（7）调用AbstractUserDetailsAuthenticationProvider.createSuccessAuthentication()修改和完善UsernamePasswordAuthenticationToken信息，比如从UserDetails拿到的Authorities信息

（8）返回UsernamePasswordAuthenticationToken

授权的核心组件：

[AccessDecisionManager] 是一个接口，定义了在授权时如何决策的方法，具体的实现类有3个：AffirmativeBased (一票通过) ，ConsensusBased (少数服从多数)，UnanimousBased (一票反对)。其中，一票通过是默认的决策。

[AbstractAccessDecisionManager] 从这个抽象类可以看出，决策的依据是是选票（Voter）的List集合。

[AccessDecisionVoter] 是一个接口，定义了vote方法，它的实现类也有很多，比如：

AuthenticatedVoter：比如某个用户对某个资源的访问是isAuthenticated()（即认证用户），该投票就通过

RoleVoter：比如某个用户对某个资源的访问是hasAnyRole("xxx")或hasRole("xxx")（即有该Role的用户），该投票就通过

我们以AffirmativeBased为例子看一下授权过程：

（1）调用AffirmativeBased.decide()方法

（2）轮训成员变量List<AccessDecisionVoter<? extends Object>> decisionVoters（在父级方法AbstractAccessDecisionManager中），如果有voter中有一个是ACCESS_GRANTED(1)，则授权通过。