Block Breaker HDU - 6699（深搜，水，写下涨涨记性）

Problem Description

Given a rectangle frame of size n×m. Initially, the frame is strewn with n×m square blocks of size 1×1. Due to the friction with the frame and each other, the blocks are stable and will not drop.

However, the blocks can be knocked down. When a block is knocked down, other remaining blocks may also drop since the friction provided by other remaining blocks may not sustain them anymore. Formally, a block will drop if it is knocked or not stable, which means that at least one of the left block and the right block has been dropped and at least one of the front block and the back block has been dropped. Especially, the frame can be regarded as a huge stable block, which means that if one block's left is the frame, only when its right block has been dropped and at least one of the front block and the back block has been dropped can it drop. The rest situations are similar.

Now you, the block breaker, want to knock down the blocks. Formally, you will do it q times. In each time, you may choose a position (xi,yi). If there remains a block at the chosen position, you will knock it down; otherwise, nothing will happen. Moreover, after knocking down the block, you will wait until no unstable blocks are going to drop and then do the next operation.

For example, please look at the following illustration, the frame is of size 2×2 and the block (1,1) and (1,2) have been dropped. If we are going to knock the block (2,2), not only itself but also the block(2,1) will drop in this knocking operation.

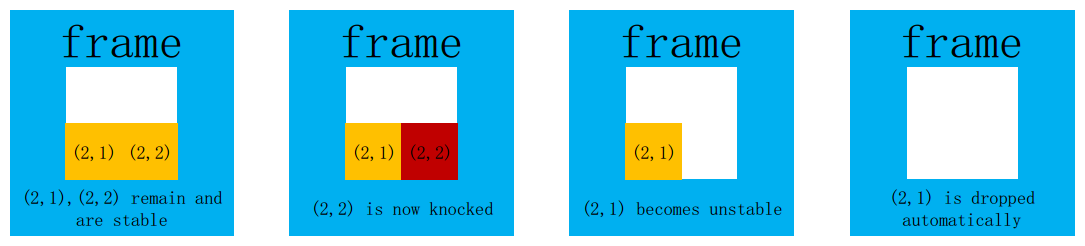
You want to know how many blocks will drop in total in each knocking operation. Specifically, if nothing happens in one operation, the answer should be regarded as 0.

Input

The first line contains one positive integer T (1≤T≤10), denoting the number of test cases.
For each test case:
The first line contains three positive integers n,m and q (1≤n,m≤2000,1≤q≤100000), denoting the sizes in two dimensions of the frame and the number of knocking operations.
Each of the following q lines contains two positive integers xi and yi (1≤xi≤n,1≤yi≤m)， describing a knocking operation.

Output

For each test case, output q lines, each of which contains a non-negative integer, denoting the number of dropped blocks in the corresponding knocking operation.

Sample Input

2
2 2 3
1 1
1 2
2 2
4 4 6
1 1
1 2
2 1
2 2
4 4
3 3

Sample Output

1

1

2
0
1

题目大意：
给出一个m*n的矩阵 q 个需要敲打的位置，矩阵里面有n*m个方块，由于与机架和其他部件的摩擦，滑块稳定，不会掉落。但是这些障碍物可以被击倒。当一个方块被击倒时，其他剩余的方块也可能掉落，因为其他剩余挡块提供的摩擦力可能不再支撑它们，如果一个区块被敲击或不稳定，它也会掉落。让我们输出每个敲打位置敲打后所掉落的方块个数。

思路：
首先要知道每个方块不能保持稳定的条件分为四种是：

1. 方块下方没有方块： 
        (1).方块左侧没有方块；
        (2).方块右侧没有方块；
  2. 方块上方没有方块：
        (1).方块左侧没有方块；
        (2).方块右侧没有方块；

所以我们只需在每个方块的上下左右做个记号即可；

PS: 我为什么错就是因为把next定义成了数组;不想说了，o(╥﹏╥)o，ε(┬┬﹏┬┬)3 哭了

详细看代码：

#include<iostream>
#include<cstdio>
using namespace std;
#define maxx 2010
int n,m;
int net[][]={,,,,-,,,-};//这里千万不要用next[];
struct node{
    int s;//记录此位置是否还有方块
    int q,d,l,r;//记录方块的上下左右是否还有方块
}a[maxx][maxx];
int dfs(int x,int y){   //进行深搜看是否还有满足掉落的方块
    int sum=;
    for(int i=;i<;i++){
        int tx=x+net[i][];
        int ty=y+net[i][];
        if(tx<=||ty<=||tx>n||ty>m||!a[tx][ty].s)
           continue;
        if((!a[tx][ty].q||!a[tx][ty].d)&&(!a[tx][ty].l||!a[tx][ty].r)){//不稳定方块的判断条件，上面有介绍;
            sum++;
          a[tx][ty].s=;
          a[tx+][ty].l=;
          a[tx-][ty].r=;
          a[tx][ty+].d=;
          a[tx][ty-].q=;
          sum+=dfs(tx,ty);
        }
    }
    return sum;
}
int main(){
    int t;
    scanf("%d",&t);
    while(t--){
        int q;
        scanf("%d%d%d",&n,&m,&q);
        for(int i=;i<=n+;i++)//为啥从“0”到“n+1”和“0”到“m+1”
        for(int j=;j<=m+;j++){//因为矩阵的四条边都是有摩擦的
         a[i][j].s=,a[i][j].d=,a[i][j].l=;
         a[i][j].r=,a[i][j].q=;
        }
        int x,y;
        for(int i=;i<=q;i++){
          int sum=;//记录掉的个数
          scanf("%d%d",&x,&y);
          if(a[x][y].s){
               sum++;
               //把与此位置有关联的方块所对应的位置标记为“0”
          a[x][y-].q=;//“下”方块的上标记为0;
          a[x+][y].l=;//同理右面的左标记为0;
          a[x-][y].r=;//左的右为0
          a[x][y+].d=;//上的下为0;
          a[x][y].s=;//掉落将其标记为0
          sum+=dfs(x,y);
          }
          printf("%d\n",sum);
        }
    }
    return ;
}