拓展kmp总结

借鉴自：https://blog.csdn.net/dyx404514/article/details/41831947

定义母串S，和子串T，设S的长度为n，T的长度为m，求T与S的每一个后缀的最长公共前缀，也就是说，设extend数组,extend[i]表示T与S[i,n-1]的最长公共前缀，要求出所有extend[i](0<=i<n)。

注意到，如果有一个位置extend[i]=m,则表示T在S中出现，而且是在位置i出现，这就是标准的KMP问题，所以说拓展kmp是对KMP算法的扩展，所以一般将它称为扩展KMP算法。

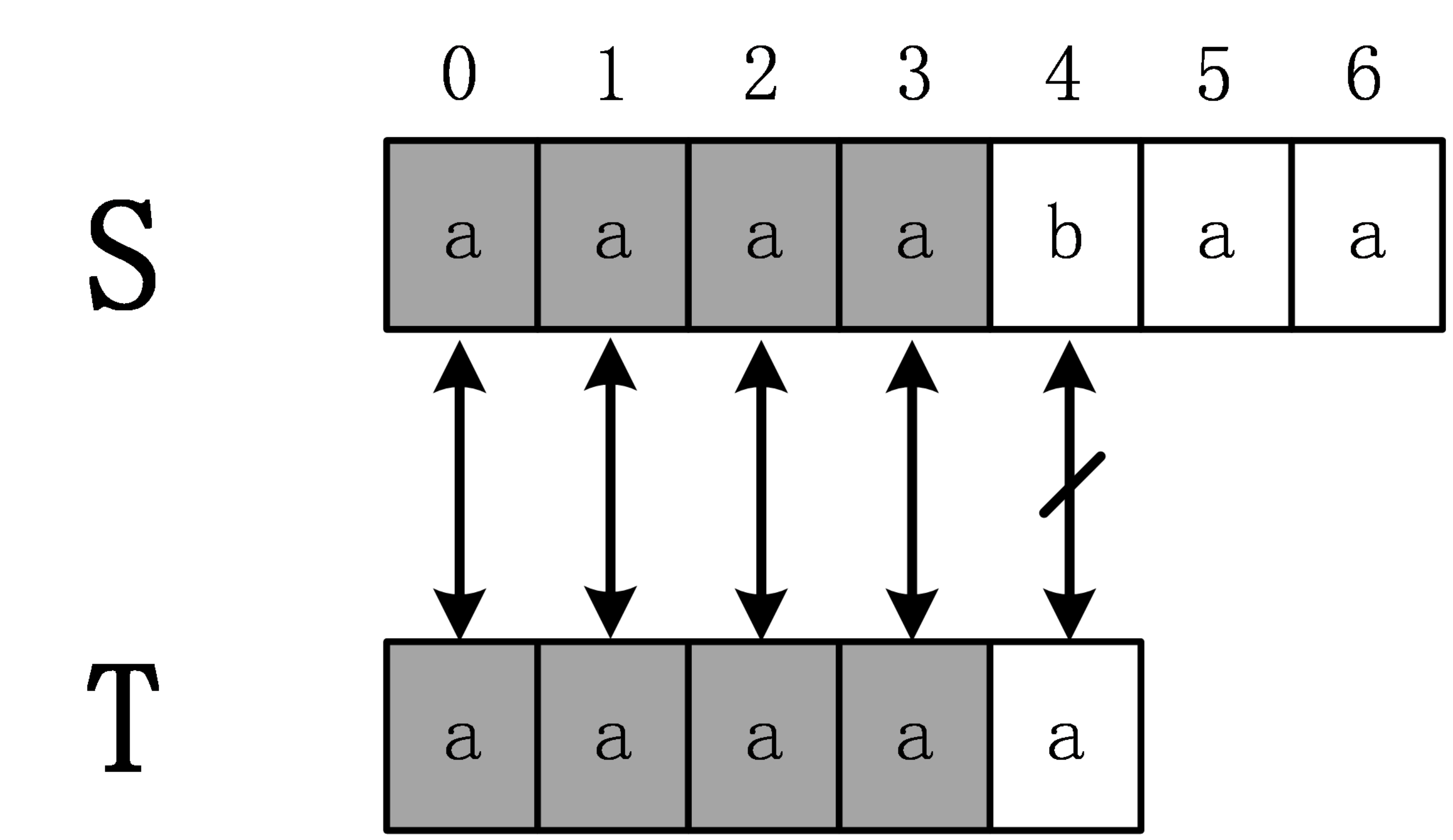
下面举一个例子，S=”aaaabaa”,T=”aaaaa”,首先，计算extend[0]时，需要进行5次匹配，直到发生失配。

从而得知extend[0]=4，下面计算extend[1],在计算extend[1]时，是否还需要像计算extend[0]时从头开始匹配呢？答案是否定的，因为通过计算extend[0]=4，从而可以得出S[0,3]=T[0,3]，进一步可以得到 S[1,3]=T[1,3],计算extend[1]时，事实上是从S[1]开始匹配，设辅助数组next[i]表示T[i,m-1]和T的最长公共前缀长度。在这个例子中，next[1]=4,即T[0,3]=T[1,4],进一步得到T[1,3]=T[0,2],所以S[1,3]=T[0,2],所以在计算extend[1]时，通过extend[0]的计算，已经知道S[1,3]=T[0,2],所以前面3个字符已经不需要匹配，直接匹配S[4]和T[3]即可，这时一次就发生失配，所以extend[1]=3。这个例子很有代表性，有兴趣的读者可以继续计算完剩下的extend数组。

1. 拓展kmp算法一般步骤

通过上面的例子，事实上已经体现了拓展kmp算法的思想，下面来描述拓展kmp算法的一般步骤。

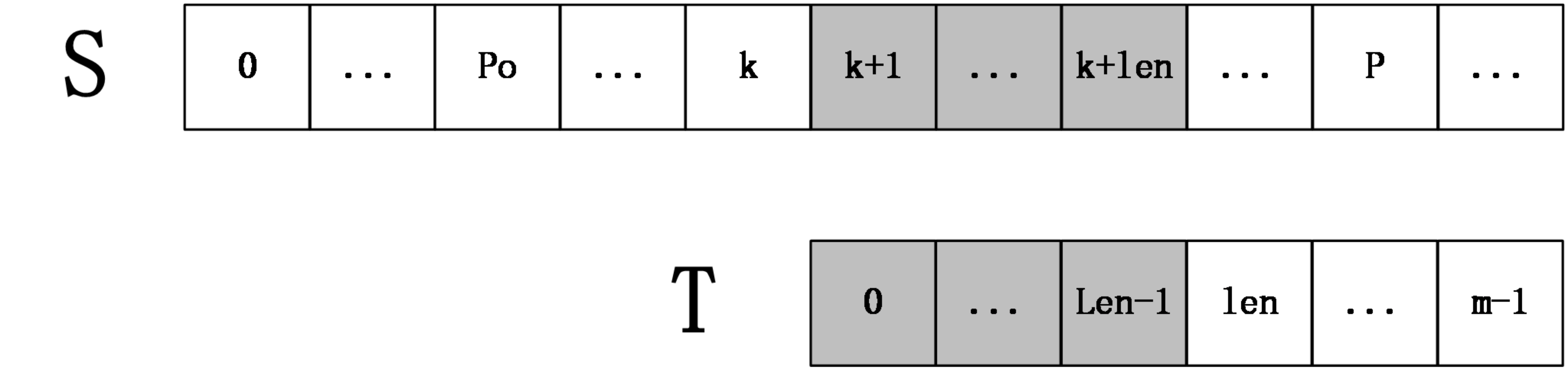
首先我们从左到右依次计算extend数组，在某一时刻，设extend[0...k]已经计算完毕，并且之前匹配过程中所达到的最远位置为P，所谓最远位置，严格来说就是i+extend[i]-1的最大值（0<=i<=k）,并且设取这个最大值的位置为po，如在上一个例子中,计算extend[1]时，P=3，po=0。

现在要计算extend[k+1],根据extend数组的定义，可以推断出S[po,P]=T[0,P-po],从而得到 S[k+1,P]=T[k-po+1,P-po],令len=next[k-po+1]，(回忆下next数组的定义next[i]表示T[i,m-1]和T的最长公共前缀长度),分两种情况讨论：

第一种情况：k+len<P

如下图所示：

上图中，S[k+1,k+len]=T[0,len-1]，然后S[k+len+1]一定不等于T[len]，因为如果它们相等，则有S[k+1,k+len+1]=T[k+po+1,k+po+len+1]=T[0,len],那么next[k+po+1]=len+1，这和next数组的定义不符(next[i]表示T[i,m-1]和T的最长公共前缀长度)，所以在这种情况下，不用进行任何匹配，就知道extend[k+1]=len。

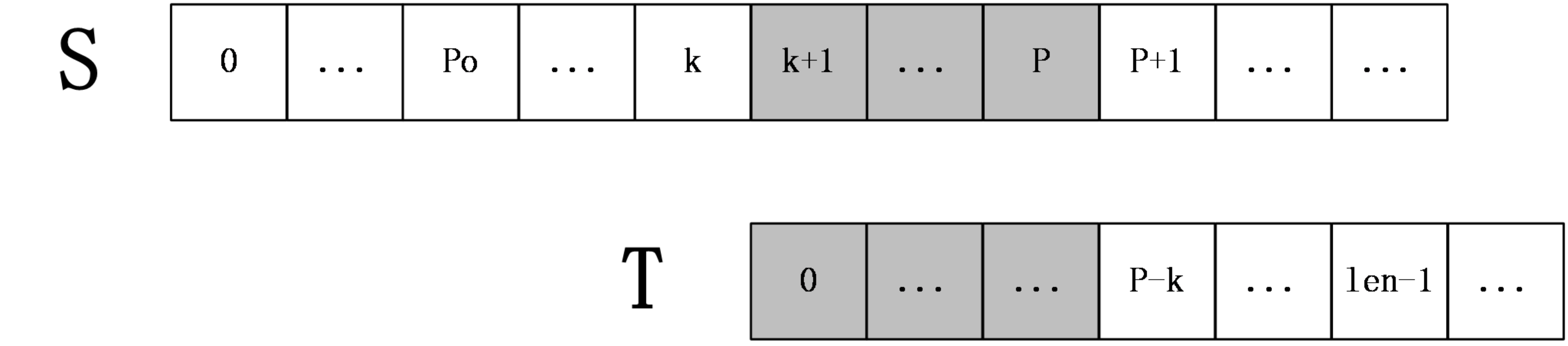
第二种情况： k+len>=P

如下图：

上图中，S[p+1]之后的字符都是未知的，也就是还未进行过匹配的字符串，所以在这种情况下，就要从S[P+1]和T[P-k+1]开始一一匹配，直到发生失配为止，当匹配完成后，如果得到的extend[k+1]+(k+1)大于P则要更新未知P和po。

至此，拓展kmp算法的过程已经描述完成，细心地读者可能会发现，next数组是如何计算还没有进行说明，事实上，计算next数组的过程和计算extend[i]的过程完全一样，将它看成是以T为母串，T为字串的特殊的拓展kmp算法匹配就可以了，计算过程中的next数组全是已经计算过的，所以按照上述介绍的算法计算next数组即可，这里不再赘述。

2. 时间复杂度分析

下面来分析一下算法的时间复杂度，通过上面的算法介绍可以知道，对于第一种情况，无需做任何匹配即可计算出extend[i]，对于第二种情况，都是从未被匹配的位置开始匹配，匹配过的位置不再匹配，也就是说对于母串的每一个位置，都只匹配了一次，所以算法总体时间复杂度是O(n)的，同时为了计算辅助数组next[i]需要先对字串T进行一次拓展kmp算法处理，所以拓展kmp算法的总体复杂度为O(n+m)的。其中n为母串的长度，m为子串的长度。

const int maxn=;   //字符串长度最大值
int next[maxn],ex[maxn]; //ex数组即为extend数组
//预处理计算next数组
void GETNEXT(char *str)
{
    int i=,j,po,len=strlen(str);
    next[]=len;//初始化next[0]
    while(str[i]==str[i+]&&i+<len)//计算next[1]
    i++;
    next[]=i;
    po=;//初始化po的位置
    for(i=;i<len;i++)
    {
        if(next[i-po]+i<next[po]+po)//第一种情况，可以直接得到next[i]的值
        next[i]=next[i-po];
        else//第二种情况，要继续匹配才能得到next[i]的值
        {
            j=next[po]+po-i;
            if(j<)j=;//如果i>po+next[po],则要从头开始匹配
            while(i+j<len&&str[j]==str[j+i])//计算next[i]
            j++;
            next[i]=j;
            po=i;//更新po的位置
        }
    }
}
//计算extend数组
void EXKMP(char *s1,char *s2)
{
    int i=,j,po,len=strlen(s1),l2=strlen(s2);
    GETNEXT(s2);//计算子串的next数组
    while(s1[i]==s2[i]&&i<l2&&i<len)//计算ex[0]
    i++;
    ex[]=i;
    po=;//初始化po的位置
    for(i=;i<len;i++)
    {
        if(next[i-po]+i<ex[po]+po)//第一种情况，直接可以得到ex[i]的值
        ex[i]=next[i-po];
        else//第二种情况，要继续匹配才能得到ex[i]的值
        {
            j=ex[po]+po-i;
            if(j<)j=;//如果i>ex[po]+po则要从头开始匹配
            while(i+j<len&&j<l2&&s1[j+i]==s2[j])//计算ex[i]
            j++;
            ex[i]=j;
            po=i;//更新po的位置
        }
    }
}

const int maxn = , INF = 0x7fffffff;
int nex[maxn], ex[maxn];

void get_next(char *s)
{
    int i=, j, po, len = strlen(s);
    nex[] = len;
    while(s[i] == s[i+] && i+ < len)
        i++;
    nex[] = i;
    po = ;
    for(int i=; i<len; i++)
    {
        if(i+nex[i-po] < po + nex[po])
            nex[i] = nex[i-po];
        else
        {
            j = po + nex[po] - i;
            if(j < ) j = ;
            while(i + j < len && s[i+j] == s[j])
                j++;
            nex[i] = j;
            po = i;
        }
    }
}

void get_ex(char *s1, char *s2)
{
    int i=, j, po, len1 = strlen(s1), len2 = strlen(s2);
    get_next(s2);
    while(s1[i] == s2[i] && i < len1 && i < len2)
        i++;
    ex[] = i;
    po = ;
    for(int i=; i<len1; i++)
    {
        if(i + nex[i - po] < po + ex[po])
            ex[i] = nex[i-po];
        else
        {
            j = po + ex[po] - i;
            if(j < ) j = ;
            while(i + j < len1 && j < len2 && s1[i+j] == s2[j])
                j++;
            ex[i] = j;
            po = i;
        }
    }
}