洛谷 P2233 [HNOI2002]公交车路线 解题报告

P2233 [HNOI2002]公交车路线

题目背景

在长沙城新建的环城公路上一共有8个公交站，分别为A、B、C、D、E、F、G、H。公共汽车只能够在相邻的两个公交站之间运行，因此你从某一个公交站到另外一个公交站往往要换几次车，例如从公交站A到公交站D，你就至少需要换3次车。

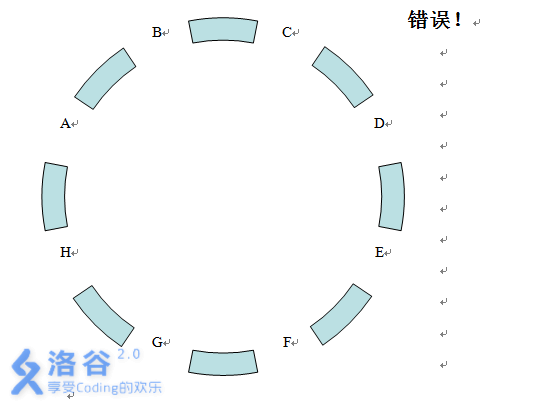
Tiger的方向感极其糟糕，我们知道从公交站A到公交E只需要换4次车就可以到达，可是tiger却总共换了n次车，注意tiger一旦到达公交站E，他不会愚蠢到再去换车。现在希望你计算一下tiger有多少种可能的乘车方案。

题目描述

输入输出格式

输入格式：

输入文件由bus.in读入，输入文件当中仅有一个正整数n(4<=n<=10000000)，表示tiger从公交车站A到公交车站E共换了n次车。

输出格式：

输出到文件bus.out。输出文件仅有一个正整数，由于方案数很大，请输出方案数除以 1000后的余数。

---

先看普通的DP做法

\(dp[i][j]\)表示换了\(i\)次车目前在\(j\)车站的方案数

转移：\(dp[i][j]=dp[i-1][j-1]+dp[i-1][j+1]\)

发现每一轮都是一样的，每一个车站也是

考虑矩阵优化

初始矩阵为(1代表出发点)

0 0 0 0 1 0 0 0 0

单次操作矩阵为

0 0 0 0 0 0 0 0 0
1 0 1 0 0 0 0 0 0
0 1 0 1 0 0 0 0 0
0 0 1 0 1 0 0 0 0
0 0 0 1 0 1 0 0 0
0 0 0 0 1 0 1 0 0
0 0 0 0 0 1 0 1 0
0 0 0 0 0 0 1 0 1
0 0 0 0 0 0 0 0 0

矩阵快速幂即可

---

Code：

#include <cstdio>
#include <cstring>
#define mod 1000
struct matrix
{
    int dx[10][10];
    matrix()
    {
        memset(dx,0,sizeof(dx));
    }
    matrix friend operator *(matrix n1,matrix n2)
    {
        matrix n3;
        for(int i=1;i<=9;i++)
            for(int j=1;j<=9;j++)
                for(int k=1;k<=9;k++)
                    n3.dx[i][j]=(n3.dx[i][j]+n1.dx[i][k]*n2.dx[k][j])%mod;
        return n3;
    }
};
matrix quick_pow(matrix d,int k)
{
    matrix f;
    for(int i=1;i<=9;i++) f.dx[i][i]=1;
    while(k)
    {
        if(k&1)
            f=f*d;
        d=d*d;
        k>>=1;
    }
    return f;
}
int main()
{
    int n;
    scanf("%d",&n);
    matrix d;
    for(int i=2;i<=8;i++)
        d.dx[i][i+1]=1;
    for(int i=2;i<=8;i++)
        d.dx[i][i-1]=1;
    d=quick_pow(d,n);
    printf("%d\n",(d.dx[5][1]+d.dx[5][9])%mod);
    return 0;
}

---

2018.7.13