分布问题(二元,多元变量分布,Beta,Dir)
这涉及到数学的概率问题。
二元变量分布:
伯努利分布,就是0-1分布(比如一次抛硬币,正面朝上概率)
那么一次抛硬币的概率分布如下:
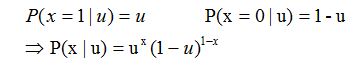
假设训练数据如下:

那么根据最大似然估计(MLE),我们要求u:

求值推导过程如下:
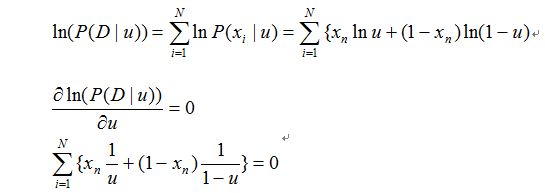
所以可以求出:
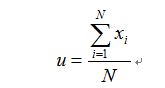
以上的推导过程就是极大似然估计,我们可以看出u就是样本出现的频率除以总共抛硬币的实验次数。但是极大似然估计有它的局限性,当训练样本比较小的时候会导致Overfitting问题,比如说抛了10次硬币,有8次朝上,那么根据极大似然估计,u的取值就应该是8/10(这符号频率派的观点)。如何解决这个问题呢?
那么这时候就需要从贝叶斯理论出发,贝叶斯理论认为,u并不是一个固定的值,u是同样服从某个分布,因此我们假设u有个先验分布P(u)。
但是如何选取这个先验分布p(u)呢?
我们知道

因此我们希望先验分布也可以有类似的概率分布,为什么这么说呢?因为后验概率=先验概率*似然函数,所以如果选择的先验分布和似然函数有一样的结构,那么得到的后验概率也会存在相似的结构,这样会使得我们后面的计算简便。
共轭性:θ的后验分布p(θ|x)与先验分布P(θ)属于同一分布,那么称二者为共轭分布。
因此我们假设u的先验分布也为

那么这时候数学里面有个分布叫做Beta分布:

那么假设我们投硬币,m次正面,l次反面。总共是m+l=N次实验:
那么这时候u的分布为:

依旧和先验分布服从一样的分布(共轭分布)
假设我们要预测下一次的实验结果,也就是给定D得到下一次的预测分布:

我们可以发现当m,N无限变大的时候,这种估计近似等于极大似然估计。
多元变量分布:
很多时候,变元的不止只有两个,还有多元,其实估计过程是类似的。 假设有k维向量,其中某个向量Xk=1,其他等于0。
例如某个变量x2发生,则X2=1,x=(0,1,0,0,0,0) 以抛筛子为例子,总共有6个面。
那么xk=1发生的概率为Uk,那么x的分布为:

考虑n个独立观测值{x1,x2,...xn}D,对应的似然函数:

其中mk其实就是这么多次实验中,uk出现的次数大小。估计极大似然估计,我们会得出:

同理,为了避免数据量小导致的过拟合问题,我们对Uk也假设一个先验分布:
考虑到对于多元变量的分布u:

因此我们选择它的共轭分布狄利克雷分布为先验分布:

那么后验分布=似然分布*先验分布:
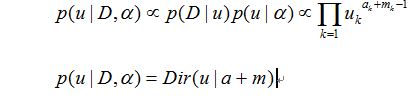
依旧和先验分布服从一样的分布(共轭分布)
假设我们要预测下一次的实验结果,也就是给定D得到下一次的预测分布:
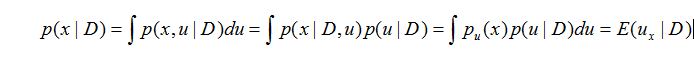
又因为对于狄利克雷分布:
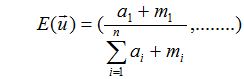
所以对于某个类的分布预测为:
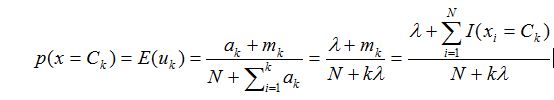
分布问题(二元,多元变量分布,Beta,Dir)的更多相关文章
- 机器学习----分布问题(二元,多元变量分布,Beta,Dir)
这涉及到数学的概率问题. 二元变量分布: 伯努利分布,就是0-1分布(比如一次抛硬币,正面朝上概率) 那么一次抛硬币的概率分布如下: 假设训练数据如下: 那么根据最大似然估计(MLE ...
- 伯努利分布、二项分布、Beta分布、多项分布和Dirichlet分布与他们之间的关系,以及在LDA中的应用
在看LDA的时候,遇到的数学公式分布有些多,因此在这里总结一下思路. 一.伯努利试验.伯努利过程与伯努利分布 先说一下什么是伯努利试验: 维基百科伯努利试验中: 伯努利试验(Bernoulli tri ...
- 关于Beta分布、二项分布与Dirichlet分布、多项分布的关系
在机器学习领域中,概率模型是一个常用的利器.用它来对问题进行建模,有几点好处:1)当给定参数分布的假设空间后,可以通过很严格的数学推导,得到模型的似然分布,这样模型可以有很好的概率解释:2)可以利用现 ...
- 【联系】—— Beta 分布与二项分布、共轭分布
1. 伯努利分布与二项分布 伯努利分布:Bern(x|μ)=μx(1−μ)1−x,随机变量 x 取值为 0,1,μ 表示取值为 1 的概率: 二项分布:Bin(m|N,μ)=(Nm)μm(1−μ)N− ...
- Memcached 笔记与总结(5)Memcached 的普通哈希分布和一致性哈希分布
普通 Hash 分布算法的 PHP 实现 首先假设有 2 台服务器:127.0.0.1:11211 和 192.168.186.129:11211 当存储的 key 经过对 2 (2 台服务器)取模运 ...
- Pytorch的默认初始化分布 nn.Embedding.weight初始化分布
一.nn.Embedding.weight初始化分布 nn.Embedding.weight随机初始化方式是标准正态分布 ,即均值$\mu=0$,方差$\sigma=1$的正态分布. 论据1——查看 ...
- T分布、卡方分布、F分布
请参考: https://www.cnblogs.com/think-and-do/p/6509239.html
- [PGM] What is Probabalistic Graphical Models
学术潜规则: 概率图模型提出的意义在于将过去看似零散的topic/model以一种统一的方式串联了起来,它便于从整体上看待这些问题,而非具体解决了某个细节. 举个例子:梯度下降,并非解决神经网络收敛问 ...
- Python Seaborn综合指南,成为数据可视化专家
概述 Seaborn是Python流行的数据可视化库 Seaborn结合了美学和技术,这是数据科学项目中的两个关键要素 了解其Seaborn作原理以及使用它生成的不同的图表 介绍 一个精心设计的可视化 ...
随机推荐
- 文件打包代码更新 使用json记录打包文件信息
经过之前的几次试验 决定使用json记录打包文件信息 #include "Package.h" #include "json/json.h" #include ...
- Redis安装部署、Jedis的使用
一.NoSQL概述 为什么需要NoSQL High performance -高并发读写 Huge Storage - 海量数据的高效率存储和访问 High Scalability && ...
- Python中ndarray数组切片问题a[-n -x:-y]
先看看如下代码: >>a=np.arange(10)>>a array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])>>a[-7:] array( ...
- 基于Web Service的客户端框架搭建二:数据转换层(FCL)
引言 要使用WebService来分离客户端与服务端,必定要使用约定好两者之间的数据契约.Json数据以其完全独立于语言的优势,成为开发者的首选.C# JavaScriptSerializer为Jso ...
- asp.net mvc 3高级编程文摘
第一章 入门 M:模型,组类,描述了要处理的数据以及修改和操作数据的业务规则 V:视图,定义应用程序用户界面的显示方式 C:控制器,一组类,用于处理来自用户,整个应用程序流以及特定应用程序逻辑的通信 ...
- C++中函数模版与类模版
1.什么是模板? (1)可以这样来解释这个问题,例如当我们需要定义多个函数,而这个函数功能其实都是一样的,例如两个数相加的函数, 只是相加的两个数的类型不相同而已,这就导致我们需要定义多个函数:当我们 ...
- PHP(四)表单的基本处理
- 试题 D: 数的分解 蓝桥杯
试题 D: 数的分解本题总分: 10 分[问题描述]把 2019 分解成 3 个各不相同的正整数之和,并且要求每个正整数都不包含数字 2 和 4,一共有多少种不同的分解方法?注意交换 3 个整数的顺序 ...
- 在ASP.NET Core2上操作MongoDB就是能这么的简便酷爽(自动完成分库分表)
NoSQL是泛指非关系型的数据库,现今在我们的项目中也多有使用,其独特的优点为我们的项目架构带来了不少亮点,而我们这里的主角(MongoDB)则是NoSQL数据库家族中的一种.事实上,NoSQL数据库 ...
- 45 Useful JavaScript Tips, Tricks and Best Practices
<45 Useful JavaScript Tips, Tricks and Best Practices> http://flippinawesome.org/2013/12/23/45 ...
