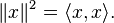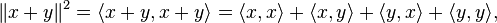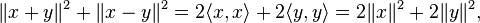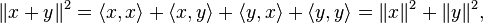parallelogram
The parallelogram law in inner product spaces
In a normed space, the statement of the parallelogram law is an equation relating norms:
In an inner product space, the norm is determined using the inner product:
As a consequence of this definition, in an inner product space the parallelogram law is an algebraic identity, readily established using the properties of the inner product:
Adding these two expressions:
as required.
If x is orthogonal to y, then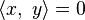 
and the above equation for the norm of a sum becomes:
which is Pythagoras' theorem.
parallelogram的更多相关文章
- Parallelogram Counting（平行四边形个数，思维转化）
1058 - Parallelogram Counting PDF (English) Statistics Forum Time Limit: 2 second(s) Memory Limit ...
- POJ 1971 Parallelogram Counting (Hash)
Parallelogram Counting Time Limit: 5000MS Memory Limit: 65536K Total Submissions: 6895 Acc ...
- 计算几何 + 统计 --- Parallelogram Counting
Parallelogram Counting Time Limit: 5000MS Memory Limit: 65536K Total Submissions: 5749 Accepted: ...
- 【codeforces 749B】Parallelogram is Back
time limit per test1 second memory limit per test256 megabytes inputstandard input outputstandard ou ...
- 1058 - Parallelogram Counting 计算几何
1058 - Parallelogram Counting There are n distinct points in the plane, given by their integer coord ...
- Codeforces 749B：Parallelogram is Back（计算几何）
http://codeforces.com/problemset/problem/749/B 题意:已知平行四边形三个顶点,求另外一个顶点可能的位置. 思路:用向量来做. #include <c ...
- Light OJ - 1058 Parallelogram Counting（判定平行四边形）
Description There are n distinct points in the plane, given by their integer coordinates. Find the n ...
- POJ 1971 Parallelogram Counting
题目链接: http://poj.org/problem?id=1971 题意: 二维空间给n个任意三点不共线的坐标,问这些点能够组成多少个不同的平行四边形. 题解: 使用的平行四边形的判断条件:对角 ...
- LightOJ 1058 - Parallelogram Counting 几何思维
http://www.lightoj.com/volume_showproblem.php?problem=1058 题意:给你顶点,问能够成多少个平行四边形. 思路:开始想使用长度来扫描有多少根,但 ...
随机推荐
- 1089. Insert or Merge (25)-判断插入排序还是归并排序
判断插入排序很好判断,不是的话那就是归并排序了. 由于归并排序区间是2.4.8开始递增的,所以要判断给出的归并排序执行到哪一步,就要k从2开始枚举. 然后再对每个子区间进行一下sort即可. #inc ...
- java实验报告五
一.实验内容 1．掌握Socket程序的编写: 2．掌握密码技术的使用: 3．设计安全传输系统. 二.实验基础: IP和端口:IP是用来标示计算机,而端口是用来标示某个计算机上面的特定应用.至于它们的 ...
- python自定义mininet拓扑
python自定义mininet拓扑 前言 闲来无聊,想到很早之前都是用GUI来自定义拓扑,这次用python来自定义一下(以前留下的苦果) 转自Mininet 自定义网络拓扑 过程相对简单 实现过程 ...
- 第三周（JAVA编写的 wordcount）
import java.io.*; public class WordCount { public static int words=1; public static int lines=1; pub ...
- JMeter学习笔记——认识JMeter（1）
拿到一个自动化测试工具,我们第一步就应该了解它能提供我们哪方面的功能(最直接的方法就是从官网获取),接下来就是简单的对这个工具进行“功能测试”了,当然这里的功能测试不是让你找它存在的bug,而是让自己 ...
- [阮一峰]Linux 守护进程的启动方法
"守护进程"(daemon)就是一直在后台运行的进程(daemon). 本文介绍如何将一个 Web 应用,启动为守护进程. 一.问题的由来 Web应用写好后,下一件事就是启动,让它 ...
- code first 如何创建索引字段
比较简单的办法: protected override void Seed(Context context) { CreateIndex(context, "ProductName" ...
- Mybatis返回HashMap时，某个字段值为null时，不会保存key
转载: http://blog.csdn.net/little2z/article/details/38525327 mybatis 的 callSettersOnNulls 问题项目用到mybati ...
- MT【175】刚刚凑巧
已知$\Delta ABC$满足$\sin^2A+\sin^2B+\sin^2C=2\sqrt{3}\sin A\sin B\sin C,a=2$,求$A$ 提示:利用正弦定理:$a^2+b^2+c^ ...
- 【USACO 1.4】Combination Lock
/* TASK:combo LANG:C++ URL:http://train.usaco.org/usacoprob2?a=E6RZnAhV9zn&S=combo SOLVE:自己做,想的是 ...