单源点最短路径的Dijkstra算法
#include<stdio.h>
#define MAXSIZE 6
#define INF 32767 void Ppath(int path[],int i,int v0)//先序递归查找最短路径(源点为v0)上的顶点
{
int k;
k=path[i];
if(k!=v0)//顶点Vk不是源点V0时
{
Ppath(path,k,v0);//递归查找顶点Vk的前一个顶点
printf("%d,",k);//输出顶点Vk
}
} void Dispath(int dist[],int path[],int s[],int v0,int n)//输出最短路径
{
int i;
for(i=;i<n;i++)
if(s[i]==)//顶点Vi在集合S中
{
printf("从%d到%d的最短路径长度为:%d,路径为:",v0,i,dist[i]);
printf("%d,",v0);//输出路径上的源点v0;
Ppath(path,i,v0);//输出路径上的中间顶点vi
printf("%d\n",i);//输出路径上的终点
}
else
printf("从%d到%d不存在路径\n",v0,i);
} void Dijkstra(int gm[][MAXSIZE],int v0,int n)//Dijkstra算法
{
int dist[MAXSIZE],path[MAXSIZE],s[MAXSIZE];
int i,j,k,mindis;
for(i=;i<n;i++)
{
dist[i]=gm[v0][i];//v0到vi的最短路径初值赋给dist[i]
s[i]=;//s[i]=0表示顶点vi属于T集
if(gm[v0][i]<INF)//路径初始化,INF为可取的最大常数
path[i]=v0;
else
path[i]=-;//v0到vi没有边
}
s[v0]=;path[v0]=;//V0并入集合S且V0当前最短路径中无前一个顶点
for(i=;i<n;i++)//对除V0外的n-1个顶点寻找最短路径,即循环n-1次
{
mindis=INF;
for(j=;j<n;j++)//从当前集合T中选择一个路径长度最短的顶点Vk
if(s[j]==&&dist[j]<mindis)
{
k=j;
mindis=dist[j];
}
s[k]=;//顶点Vk加入集合S中
for(j=;j<n;j++)//调整源点v0到集合T中任一顶点Vj的路径长度
if(s[j]==)//顶点vj在集合T中
if(gm[k][j]<INF&&dist[k]+gm[k][j]<dist[j])//当V0到Vj的路径长度小于V0到Vk和Vk到Vj的路径长度时
{
dist[j]=dist[k]+gm[k][j];
path[j]=k;//Vk是当前最短路径中Vj的前一个顶点
}
}
Dispath(dist,path,s,v0,n);//输出最短路径
} void main()
{
int g[MAXSIZE][MAXSIZE]={{INF,,,INF,INF,INF},{,INF,INF,INF,,},{INF,,INF,INF,INF,},
{INF,INF,INF,INF,INF,INF},{INF,INF,INF,,INF,INF},{INF,INF,INF,,,INF}};//定义邻接矩阵g
Dijkstra(g,,);//求顶点0的最短路径
}
输出:
带权有向图及邻接矩阵示意: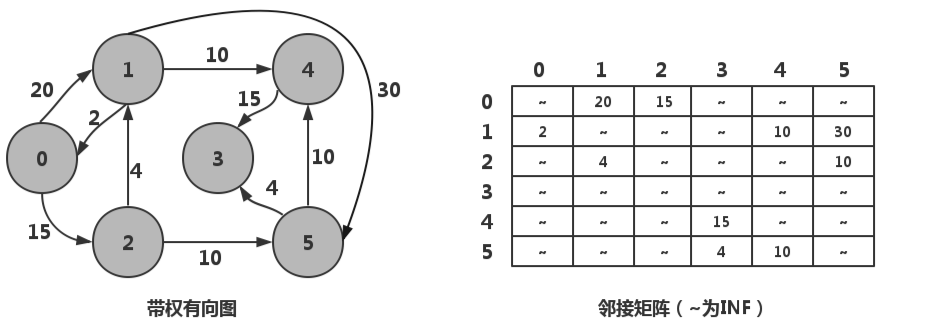
单源点最短路径的Dijkstra算法的更多相关文章
- 单源最短路径(dijkstra算法)php实现
做一个医学项目,当中在病例评分时会用到单源最短路径的算法.单源最短路径的dijkstra算法的思路例如以下: 如果存在一条从i到j的最短路径(Vi.....Vk,Vj),Vk是Vj前面的一顶点.那么( ...
- 【算法设计与分析基础】25、单起点最短路径的dijkstra算法
首先看看这换个数据图 邻接矩阵 dijkstra算法的寻找最短路径的核心就是对于这个节点的数据结构的设计 1.节点中保存有已经加入最短路径的集合中到当前节点的最短路径的节点 2.从起点经过或者不经过 ...
- 【算法导论】单源最短路径之Dijkstra算法
Dijkstra算法解决了有向图上带正权值的单源最短路径问题,其运行时间要比Bellman-Ford算法低,但适用范围比Bellman-Ford算法窄. 迪杰斯特拉提出的按路径长度递增次序来产生源点到 ...
- 单源最短路径:Dijkstra算法(堆优化)
前言:趁着对Dijkstra还有点印象,赶快写一篇笔记. 注意:本文章面向已有Dijkstra算法基础的童鞋. 简介 单源最短路径,在我的理解里就是求从一个源点(起点)到其它点的最短路径的长度. 当然 ...
- 单源最短路径问题-Dijkstra算法
同样是层序遍历,在每次迭代中挑出最小的设置为已知 ===================================== 2017年9月18日10:00:03 dijkstra并不是完全的层序遍历 ...
- 0016:单源最短路径(dijkstra算法)
题目链接:https://www.luogu.com.cn/problem/P4779 题目描述:给定一个 n 个点,m 条有向边的带非负权图,计算从 s 出发,到每个点的距离. 这道题就是一个单源最 ...
- 单源最短路径问题(dijkstra算法 及其 优化算法(优先队列实现))
#define _CRT_SECURE_NO_WARNINGS /* 7 10 0 1 5 0 2 2 1 2 4 1 3 2 2 3 6 2 4 10 3 5 1 4 5 3 4 6 5 5 6 9 ...
- Dijkstra单源点最短路径算法
学习参考: Dijkstra算法(单源最短路径) 最短路径—Dijkstra算法和Floyd算法 使用的图结构: 邻接矩阵: -1 20 -1 25 80-1 -1 40 -1 -1-1 -1 -1 ...
- Bellman-Ford & SPFA 算法——求解单源点最短路径问题
Bellman-Ford算法与另一个非常著名的Dijkstra算法一样,用于求解单源点最短路径问题.Bellman-ford算法除了可求解边权均非负的问题外,还可以解决存在负权边的问题(意义是什么,好 ...
随机推荐
- python 栈和队列
class Stack: def __init__(self): self.items = [] def isEmpty(self): return self.items == [] def push ...
- 【updating】python读书笔记-The Django Book2.0(for django1.4)
原文:http://www.djangobook.com/en/2.0/frontmatter.html 译文:http://djangobook.py3k.cn/2.0/ 或者http://docs ...
- mybatis 热部署xml文件(spring boot和springmvc两种方式)
参考:http://thinkgem.iteye.com/blog/2304557 步骤:1.创建两个java类 (1)MapperRefresh.java :用于刷新mapper (2)SqlS ...
- Spring 学习笔记之整合Hibernate
Spring和Hibernate处于不同的层次,Spring关心的是业务逻辑之间的组合关系,Spring提供了对他们的强大的管理能力, 而Hibernate完成了OR的映射,使开发人员不用再去关心SQ ...
- intellij idea 破解补丁激活
一.说明 idea激活可以用JetBrains account,Activation Code注册码或者填License server网址,使用注册码的方式可以参考lanyun提供的注册码,但是有效时 ...
- Linux修改服务器ip
Linux基础二(修改ip地址.修改网关.修改DNS服务器.重新启动网络配置) 网络的初始化 .ip地址的修改(临时生效) 使用ifconfig命令 ifconfig 网卡名 ip地址 netma ...
- POJ 3279 Fliptile ( 开关问题)
题目链接 Description Farmer John knows that an intellectually satisfied cow is a happy cow who will give ...
- Linux 入门记录:一、命令行 Bash 的基本操作
为了以后长期的线上测试和服务器的性能考量,要用 Linux 服务器了.昨晚装了个 CentOS 6.9,今天开始学学 Linux 基础,扫扫盲.ok,小本本记 ing... 一.Shell简介 She ...
- 移动端测试===Android内存管理: 理解App的PSS
Android内存管理: 理解App的PSS 原文链接:http://www.littleeye.co/blog/2013/06/11/android-memory-management-unders ...
- VPS性能综合测试(6):UnixBench跑分工具测试
测试时间可能会比较长,请耐心等待.最后UnixBench会详细列出各个测试项目的得分情况,以及VPS性能的综合跑分结果 UinxBench 的使用 使用方法如下: Run [ -q | -v ] [- ...
