LeetCode-Subsets ZZ

LeetCode:Subsets

Given a set of distinct integers, S, return all possible subsets.

Note:

• Elements in a subset must be in non-descending order.
• The solution set must not contain duplicate subsets.

For example,
If S = [1,2,3], a solution is:

[
  [3],
  [1],
  [2],
  [1,2,3],
  [1,3],
  [2,3],
  [1,2],
  []
]                                                                                                             本文地址

分析：求集合的所有子集问题。题目要求子集中元素非递减序排列，因此我们先要对原来的集合进行排序。原集合中每一个元素在子集中有两种状态：要么存在、要么不存在。这样构造子集的过程中每个元素就有两种选择方法：选择、不选择，因此可以构造一颗二叉树，例如对于例子中给的集合[1,2,3]，构造的二叉树如下（左子树表示选择该层处理的元素，右子树不选择），最后得到的叶子节点就是子集：

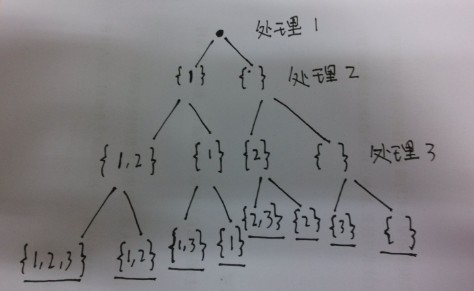
算法1：根据上面的启发，我们可以用dfs来得到树的所有叶子节点，代码如下：

 1 class Solution {
 2 private:
 3     vector<vector<int> >res;
 4 public:
 5     vector<vector<int> > subsets(vector<int> &S) {
 6         // IMPORTANT: Please reset any member data you declared, as
 7         // the same Solution instance will be reused for each test case.
 8         //先排序，然后dfs每个元素选或者不选，最后叶子节点就是所有解
 9         res.clear();
10         sort(S.begin(), S.end());
11         vector<int>tmpres;
12         dfs(S, 0, tmpres);
13         return res;
14     }
15     void dfs(vector<int> &S, int iend, vector<int> &tmpres)
16     {
17         if(iend == S.size())
18             {res.push_back(tmpres); return;}
19         //选择S[iend]
20         tmpres.push_back(S[iend]);
21         dfs(S, iend+1, tmpres);
22         tmpres.pop_back();
23         //不选择S[iend]
24         dfs(S, iend+1, tmpres);
25     }
26 };

算法2：从上面的二叉树可以观察到，当前层的集合 = 上一层的集合 + 上一层的集合加入当前层处理的元素得到的所有集合（其中树根是空集），因此可以从第二层开始（第一层是空集合）迭代地求最后一层的所有集合（即叶子节点），代码如下：

 1 class Solution {
 2 public:
 3     vector<vector<int> > subsets(vector<int> &S) {
 4     // IMPORTANT: Please reset any member data you declared, as
 5     // the same Solution instance will be reused for each test case.
 6     int len = S.size();
 7     sort(S.begin(), S.end());
 8     vector<vector<int> > res(1);//开始加入一个空集
 9     for(int i = 0; i < len; ++i)
10     {
11         int resSize = res.size();
12         for(int j = 0; j < resSize; j++)
13         {
14             res.push_back(res[j]);
15             res.back().push_back(S[i]);
16         }
17     }
18     return res;
19 }
20 };

算法3：可以根据二进制的思想，比如对于3个元素的集合，000表示一个元素都不选择，001表示选择第一个元素，101表示选择第一个和第三个元素...。因此如果集合大小为n，我们只需要让一个整数从0逐渐增加到2^n-1, 每个整数的二进制形式可以表示一个集合。如果用整数的二进制表示集合，这个算法有个限制，最大能表示集合元素的个数为64（unsigned long long）。如果使用bitmap，然后模拟二进制的加1操作，则对集合大小就没有限制。刚好这一题集合的大小不超过64

 1 class Solution {
 2 public:
 3     vector<vector<int> > subsets(vector<int> &S) {
 4     // IMPORTANT: Please reset any member data you declared, as
 5     // the same Solution instance will be reused for each test case.
 6     int len = S.size();
 7     sort(S.begin(), S.end());
 8     vector<vector<int> > res(1);//开始加入一个空集
 9
10     unsigned long long bit = 1, bitmax = (1<<len);
11     vector<int> tmpres;
12     while(bit < bitmax)
13     {
14         tmpres.clear();
15         unsigned long long curBit = bit;
16         for(int i = 0; i < len; i++)//依次检测前len个二进制位
17         {
18             if(curBit & 1)
19                 tmpres.push_back(S[i]);
20             curBit >>= 1;
21         }
22         res.push_back(tmpres);
23         bit++;
24     }
25     return res;
26 }
27 };

---

LeetCode:Subsets II

Given a collection of integers that might contain duplicates, S, return all possible subsets.

Note:

• Elements in a subset must be in non-descending order.
• The solution set must not contain duplicate subsets.

For example,
If S = [1,2,2], a solution is:

[
  [2],
  [1],
  [1,2,2],
  [2,2],
  [1,2],
  []
]

分析：在上一题的基础上，可以允许集合中包含重复元素，我们也把相应的二叉树画出类，以集合{1,2,2}举例

算法1：dfs解法。注意到处理第三个元素2时，因为前面已经处理了一次2，所有第三层中，我们只在已经添加过2的集合{1,2}、{2}上再添加2，而没有在集合{1}, {}上添加2（画叉叉的那么分支），假设下面还有一个2，那么我们只在第四层的包含两个2的集合{1,2,2}、{2,2}上再添加2，其它都不添加。因此dfs时，如果当前处理的数字前面出现了k次，那么我们要处理的集合中必须包含k个该元素。代码如下：

 1 class Solution {
 2 private:
 3     vector<vector<int> >res;
 4 public:
 5     vector<vector<int> > subsetsWithDup(vector<int> &S) {
 6         // IMPORTANT: Please reset any member data you declared, as
 7         // the same Solution instance will be reused for each test case.
 8         //先排序，然后dfs每个元素选或者不选，最后叶子节点就是所有解
 9         res.clear();
10         sort(S.begin(), S.end());
11         vector<int>tmpres;
12         dfs(S, 0, tmpres);
13         return res;
14     }
15     void dfs(vector<int> &S, int iend, vector<int> &tmpres)
16     {
17         if(iend == S.size())
18             {res.push_back(tmpres); return;}
19         int firstSame = iend;
20         while(firstSame >=0 && S[firstSame] == S[iend])firstSame--;
21         firstSame++; //firstSame是第一个和S[iend]相同数字的位置
22         int sameNum = iend - firstSame;//和S[iend]相同数字的个数(除自己)
23         if(sameNum == 0 ||
24             (tmpres.size() >= sameNum && tmpres[tmpres.size() - sameNum] == S[iend]))
25         {
26             //选择S[iend]
27             tmpres.push_back(S[iend]);
28             dfs(S, iend+1, tmpres);
29             tmpres.pop_back();
30         }
31         //不选择S[iend]
32         dfs(S, iend+1, tmpres);
33     }
34 };

算法2：在上一题算法2的基础上，如果当前处理的元素没有出现过，则把前面得到的所有集合加上该元素；如果出现过，则只把上一轮处理的集合加上该元素。比如处理第二个2时（二叉树第三层），我们只把上一轮添加过数字的集合{1,2}、{2}再添加一个2加入结果中，{1}、{}是从上一层直接继承下来的，所以不作处理。代码如下：

 1 class Solution {
 2 private:
 3     vector<vector<int> >res;
 4 public:
 5     vector<vector<int> > subsetsWithDup(vector<int> &S) {
 6         // IMPORTANT: Please reset any member data you declared, as
 7         // the same Solution instance will be reused for each test case.
 8         int len = S.size();
 9         sort(S.begin(), S.end());
10         vector<vector<int> > res(1);//开始加入一个空集
11         int last = S[0], opResNum = 1;//上一个数字、即将要进行操作的子集数量
12         for(int i = 0; i < len; ++i)
13         {
14             if(S[i] != last)
15             {
16                 last = S[i];
17                 opResNum = res.size();
18             }
19             //如果有重复数字，即将操作的子集的数目和上次相同
20             int resSize = res.size();
21             for(int j = resSize-1; j >= resSize - opResNum; j--)
22             {
23                 res.push_back(res[j]);
24                 res.back().push_back(S[i]);
25             }
26         }
27         return res;
28     }
29 };

上一题基于二进制思想的算法3不适合于包含重复元素的集合

【版权声明】转载请注明出处：http://www.cnblogs.com/TenosDoIt/p/3451902.html