【洛谷】P1196 银河英雄传说（并查集）

题目描述

公元五八○一年，地球居民迁至金牛座α第二行星，在那里发表银河联邦创立宣言，同年改元为宇宙历元年，并开始向银河系深处拓展。

宇宙历七九九年，银河系的两大军事集团在巴米利恩星域爆发战争。泰山压顶集团派宇宙舰队司令莱因哈特率领十万余艘战舰出征，气吞山河集团点名将杨威利组织麾下三万艘战舰迎敌。

杨威利擅长排兵布阵，巧妙运用各种战术屡次以少胜多，难免恣生骄气。在这次决战中，他将巴米利恩星域战场划分成30000列，每列依次编号为1, 2, …,30000。之后，他把自己的战舰也依次编号为1, 2, …, 30000，让第i号战舰处于第i列(i = 1, 2, …, 30000)，形成“一字长蛇阵”，诱敌深入。这是初始阵形。当进犯之敌到达时，杨威利会多次发布合并指令，将大部分战舰集中在某几列上，实施密集攻击。合并指令为M i j，含义为第i号战舰所在的整个战舰队列，作为一个整体（头在前尾在后）接至第j号战舰所在的战舰队列的尾部。显然战舰队列是由处于同一列的一个或多个战舰组成的。合并指令的执行结果会使队列增

大。然而，老谋深算的莱因哈特早已在战略上取得了主动。在交战中，他可以通过庞大的情报网络随时监听杨威利的舰队调动指令。

在杨威利发布指令调动舰队的同时，莱因哈特为了及时了解当前杨威利的战舰分布情况，也会发出一些询问指令：C i j。该指令意思是，询问电脑，杨威利的第i号战舰与第j号战舰当前是否在同一列中，如果在同一列中，那么它们之间布置有多少战舰。

作为一个资深的高级程序设计员，你被要求编写程序分析杨威利的指令，以及回答莱因哈特的询问。

最终的决战已经展开，银河的历史又翻过了一页……

输入输出格式

输入格式：

输入文件galaxy.in的第一行有一个整数T（1<=T<=500,000），表示总共有T条指令。

以下有T行，每行有一条指令。指令有两种格式：

M i j ：i和j是两个整数（1<=i , j<=30000），表示指令涉及的战舰编号。该指令是莱因哈特窃听到的杨威利发布的舰队调动指令，并且保证第i号战舰与第j号战舰不在同一列。
C i j ：i和j是两个整数（1<=i , j<=30000），表示指令涉及的战舰编号。该指令是莱因哈特发布的询问指令。

输出格式：

输出文件为galaxy.out。你的程序应当依次对输入的每一条指令进行分析和处理：

如果是杨威利发布的舰队调动指令，则表示舰队排列发生了变化，你的程序要注意到这一点，但是不要输出任何信息；

如果是莱因哈特发布的询问指令，你的程序要输出一行，仅包含一个整数，表示在同一列上，第i 号战舰与第j 号战舰之间布置的战舰数目。如果第i 号战舰与第j号战舰当前不在同一列上，则输出-1。

输入输出样例

输入样例#1：复制

输出样例#1：复制

-1

1

说明

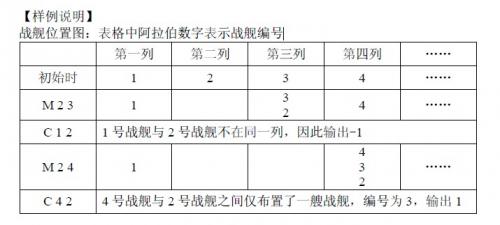
【样例说明】

战舰位置图：表格中阿拉伯数字表示战舰编号

-----------------------------------------------------------------------------------------------------------------

分析：很妙的一题啊！关键是如何快速维护战舰之间的关系。

　　算法1（30分）：由于路径压缩会破坏舰船之间的距离，所以我们就不路径压缩了，直接查询路上有几个战舰。

　　算法2（100分）：考虑到楼上那玩意在n=30000，t=500000的情况下就是作死，所以我们必须路径压缩，那么如何维护战舰之间的距离呢？用front[i]表示飞船i与其所在列队头的距离，num[i]表示第i列的飞船数量，这样传递时只需要改变这两个数组，就可以放心的路径压缩了。至于如何传递时改变，请看我代码：

#include <cstdio>

#include <cmath>

#include <algorithm>

using namespace std;

const int maxn=;

int pa[maxn],num[maxn],front[maxn];

//fa[i]表示飞船i的祖先

//front[i]表示飞船i与其所在列队头的距离

//num[i]表示第i列的飞船数量

void init()

{

    for(int i=;i<maxn;i++)

    {

        pa[i]=i;

        num[i]=;

    }

}

int find(int x)

{

    if(pa[x]==x) return x;

    else

    {

        int k=find(pa[x]);

        front[x]+=front[pa[x]];//把距离不断加上去

        return pa[x]=k;

    }

}

void unite(int x,int y)

{

    x=find(x);y=find(y);

    front[x]+=num[y];

    pa[x]=y;

    num[y]+=num[x];

    num[x]=;

}

bool same(int x,int y)

{

    return find(x)==find(y);

}

int main()

{

    init();

    int t,a,b;

    char s[];

    scanf("%d",&t);

    for(int i=;i<t;i++)

    {

        scanf("%s%d%d",s,&a,&b);

        if(s[]=='M') unite(a,b);

        else

        {

            if(!same(a,b)) printf("-1\n");

            else printf("%d\n",abs(front[a]-front[b])-);

        }

    }

    return ;

}