图论：Tarjan算法

　　在有向图中，若两点至少包含一条路径可以到达，则称两个顶点强连通，若任意两个顶点皆如此，则称此图为强联通图。非强连通图有向图的极大强连通子图，称为强连通分量(strongly connected components)。

　　

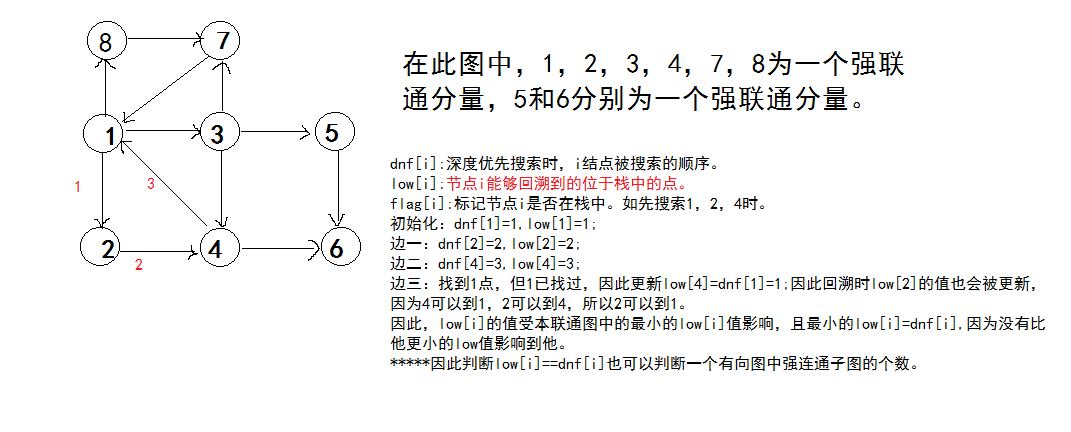
　　中间查找过程类似于深度优先搜索和并查集。

代码实现：

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
#include <queue>
#include <stack>
#include <cstdlib>
#include <iomanip>
#include <cmath>
#include <cassert>
#include <ctime>
#include <cstdlib>
#include <map>
#include <set>
using namespace std;
#pragma comment(linker, "/stck:1024000000,1024000000")
#define lowbit(x) (x&(-x))
#define max(x,y) (x>=y?x:y)
#define min(x,y) (x<=y?x:y)
#define MAX 100000000000000000
#define MOD 1000000007
#define pi acos(-1.0)
#define ei exp(1)
#define PI 3.1415926535897932384626433832
#define ios() ios::sync_with_stdio(true)
#define INF 1044266558
#define mem(a) (memset(a,0,sizeof(a)))
typedef long long ll;
int dnf[],low[],pos[],vis[];
int n,k=-,g[][],ans=,m,num=;
void tarjan(int u)
{
    dnf[u]=low[u]=ans++;
    pos[++k]=u;
    vis[u]=;
    for(int i=;i<=n;i++)
    {
        if(g[u][i])
        {
            if(!dnf[i])
            {
                tarjan(i);
                low[u]=min(low[u],low[i]);
            }
            else
            {
                if(vis[i]) low[u]=min(dnf[u],low[i]);
            }
        }
    }
    int cnt;
    if(dnf[u]==low[u])
    {
        printf("Case #%d: ",++num);
        do
        {
            cnt=pos[k--];
            printf("%d ",cnt);
            vis[cnt]=;
        }while(cnt!=u);
        printf("\n");
    }
}
int main()
{
    scanf("%d%d",&n,&m);
    memset(g,,sizeof(g));
    memset(dnf,,sizeof(dnf));
    memset(low,,sizeof(low));
    memset(pos,,sizeof(pos));
    for(int i=;i<m;i++)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        g[x][y]=;
    }
    printf("\n\n");
    tarjan();
    printf("************************\n");
    printf("The number of the strongly connected components: %d\n",num);
    printf("************************\n");
    for(int i=;i<=n;i++)
    {
        printf("dnf[%d]:%d  low[%d]:%d\n",i,dnf[i],i,low[i]);
    }
    return ;
}
/*
8 12
1 3
1 2
1 8
8 7
7 1
3 7
2 4
4 1
3 4
3 5
4 6
5 6
 */